|
“Digital
Signal Processing” No. 2-2019 |
|
Vector and spectral digital signal processing in musical acoustics by the method of parametric discrete Fourier transform
N.V., Smirnova., Sevastopol State University (SevSU) Russia, Sevastopol, e-mail: yolkanv@gmail.com
O.V. Ponomareva, Kalashnikov Izhevsk State Technical University (IzhSTU), Russia, Izhevsk, ponva@mail.ru
Keywords: musical acoustics, musical signal, discrete Fourier transform, parametric discrete Fourier transform, digital information music technologies, localization of spectral peaks, pitch, timbre.
Abstract
The article discusses one of the current scientific areas of digital signal processing (DSP) - digital vector and spectral processing of music signals, which play an important role in digital information music technologies. The main tasks of vector and spectral processing of signals in musical acoustics are to determine the pitch and timbre of emmelic musical sounds, since it is these characteristics of musical signals that make it possible to judge the melody, harmony, sounding voice and instrument.
A system analysis of the methods of vector and spectral processing of musical signals used in musical acoustics has shown the widespread use of classical methods based on discrete Fourier transform (DFT) and algorithms for its fast calculation - fast Fourier transform (FFT) algorithms. This is explained by the adequacy of the DFT mathematical apparatus to the structure of musical signals, the possibility of visual physical interpretation and interpretation of the results. At the same time, the DFT, in addition to its advantages, also has significant drawbacks, which are manifested in the form of undesirable effects of superposition, stockade, leakage, and scallop effect. When processing musical signals, the effect of the picket is especially undesirable, which impedes the processing of signals due to the mismatch of the frequencies of musical sounds and their overtones with the frequencies obtained as a result of using DFT.
The article considers a generalization of the discrete Fourier transform in the form of a parametric discrete Fourier transform (DFT-P). This conversion allows you to eliminate or significantly reduce the effect of undesirable effects of DFT in vector and spectral processing of signals. The article shows that the use of DFT-P instead of DFT allows one to obtain a more detailed spectral picture, both in statics and dynamics. The fact is that both the vector and spectral patterns obtained using the DFT are only “thinned out” versions of the corresponding pictures obtained on the basis of the DFT-P.
It is proposed to increase the efficiency and effectiveness of the methods of spectral and vector processing of musical signals in musical acoustics through the application of the method of parametric Fourier transform (DFT-P). The problems of using DFT-P to determine the fundamental tone and timbre of musical signals are investigated.
References
1. Ponomareva O.V. Razvitie teorii spektral'nogo analiza diskretnyh signalov na konechnyh intervalah v bazise parametricheskih eksponencial'nyh funkcij (Development of the theory of spectral analysis of discrete signals at finite intervals in the basis of parametric exponential functions) // Digital Signal Processing. 2010. no. 2. pp. 7 - 11.
2. Ponomarev V.A., Ponomareva O.V. Teoriya i primenenie parametricheskogo diskretnogo preobrazovaniya Fur'e (Theory and application of the parametric discrete Fourier transform) // Digital signal processing. 2011. no. 1. pp. 2 - 6.
3. Ponomarev V.A. Ponomareva O.V., Ponomarev A.V. Method for Effective Measurement of a Sliding Parametric Fourier Spectrum. Optoelectronics, Instrumentation and Data Processing, vol. 50, no. 2, pp.1-7. (2014).
4. Ponomareva O.V. Osnovy teorii diskretnyh kosvennyh izmerenij parametrov signalov (Fundamentals of the theory of discrete indirect measurements of signal parameters). Izhevsk. Publishing house IzhSTU/ 2016. 172 p.
5. Ponomareva O., Ponomarev A., Ponomarev V. Evolution of Forward and Inverse Discrete Fourier Transform // Proceedings of IEEE East-West Design & Test Symposium (EWDTS 2018). 2018. C. 313-318.
6. Ponomareva O., Ponomarev A., Ponomareva N. Window - presume Parametric Discrete Fourier Transform // Proceedings of IEEE East-West Design & Test Symposium (EWDTS 2018). 2018. C. 364-368.
7. Ponomareva, O.V. Razvitie teorii i razrabotka metodov i algoritmov cifrovoj obrabotki informacionnyh signalov v parametricheskih bazisah Fur'e (The development of theory and the development of methods and algorithms for digital processing of information signals in parametric Fourier bases) Âis .... Dr. tech. Sciences: 05.13.01 / Ponomareva Olga Vladimirovna. - Izhevsk, 2016 .-- 357 p.
8. Aldoshina, I.A. Muzykal'naya akustika: uchebnik / I.A.Aldoshina, R.Pritts (Musical acoustics: textbook / I.A. Aldoshina, R. Pritts) SPb: Kompozitor – Sankt-Peterburg. 2006. 720 p.
9. Aldoshina, I.A. Osnovy psihoakustiki. (Fundamentals of psychoacoustics ) Podborka statej s sajta http://www.625-net.ru.CH.1-17. 154 p. Rezhim dostupa: http:/www.twirpx.com/file/141630/
10. Ponomareva, N. V. Komp'yuternaya spektral'naya obrabotka muzykal'no-akusticheskih signalov na osnove parametricheskogo diskretnogo preobrazovaniya Fur'e (Computer-aided spectral processing of musical acoustic signals based on the parametric discrete Fourier transform) // Priborostroenie - 2017: materialy 10-j Mezhdunarodnoj nauchno-tekhnicheskoj konferencii, 1-3 noyabrya 2017 goda, Minsk, Respublika Belarus' / Belorusskij nacional'nyj tekhnicheskij universitet; redkol.: O. K. Gusev [i dr.]. Minsk: BNTU/ 2017. pp. 16-18.
11. Ponomareva, N. V. Problemy komp'yuternoj spektral'noj obrabotki signalov v muzykal'noj akustike (Problems of computer spectral processing of signals in musical acoustics) // Intellektual'nye sistemy v proizvodstve. 2018. vol. 16. no 1. pp.. 26-32.
12. Kuznecov, L.A. Akustika muzykal'nyh instrumentov: Spravochnik (Acoustics of Musical Instruments: A Guide) // M. Legprombytizdat, 1989.– 368 p.
13. Petelin R.YU. Yu.V. Petelin Zvukovaya studiya v PC (Sound Studio in PC)// SPb.:BHV-Sankt-Peterburg 1998. 256 p.
14. Cvetkov, E.I. Osnovy matematicheskoj metrologii (Fundamentals of Mathematical Metrology) // SPb. Politekhnika. 2005.-510 p.
15. Rabiner L., Gold B. Theory and Application of digital signal processing. New Jersey, Prentice-hall, 1975, 772 p.
Fundamentals of the theory of two-dimensional digital signal processing in Fourier bases with variable parameters
A.V. Ponomarev
Kalashnikov Izhevsk State Technical University (IzhSTU), Russia, Izhevsk, e-mail: ponva@mail.ru
Keywords: two-dimensional discrete Fourier transform, cyclic two-dimensional correlation function, spatial domain, spatial frequency domain, canonical decomposition of a random signal.
Abstract
The article discusses the basics of the theory of two-dimensional digital processing of signals specified on a finite reference plane in Fourier bases with variable parameters. Currently, there is not only an expansion in the areas of application of digital signal processing methods, but also a significant complication of the tasks to be solved, in particular, a transition from methods of spectral processing of one-dimensional signals (1-D signals) to methods of spectral processing of two-dimensional signals (2-D signals) to based on a two-dimensional discrete Fourier transform (2-D DFT).
The theory under development is a generalization of the classical theory of discrete two-dimensional spectral processing of signals specified on a finite reference plane in Fourier bases. When conducting 2-D correlation analysis, 2-D signal filtering, and 2-D spectral and vector processing of 2 D signals, the operation of supplementing the 2-D signal on the reference plane with zero samples is widely used. Based on the analysis of structural modification of the 2-D DFT matrix, in the case of supplementing the 2-D signal on the reference plane with zero samples, a system of 2-D parametric discrete exponential functions (2-D DEF-P) is introduced. The analytical properties of the 2-D DEF-P system, which is the basis of the newly introduced direct two-dimensional parametric discrete Fourier transform (2-D DFT-P), are considered.
The theoretical foundations of the proposed theory allow us to develop new and improve existing methods and algorithms of two-dimensional Fourier - signal processing, as well as eliminate or significantly reduce the effects of negative effects accompanying the use of standard 2-D DFT. The proposed two-dimensional DFT-P significantly expands the mathematical apparatus of information technology methods for digital spectral processing of signals and images in the spatial and spatial-frequency domains.
Studies of the analytical properties of 2-D DEF-P, which are the basis of 2-D DFT-P, allow us to conclude that the probabilistic properties of 2-D DFT-P of two-dimensional signals - the properties that follow from the two-dimensional version of the Wiener-Khinchin theorem - are promising.
References
1. Ponomarev V.A., Ponomareva O.V. Vibroakusticheskoe diagnostirovanie korobok peredach stankov cifrovymi metodami (Vibroacoustic diagnosis of machine gearboxes by digital methods) // Machine tools and tools. 1983..no. 9.pp.. 18 - 21.
2. Ponomarev V.A., Ponomareva O.V. Vremennye okna pri ocenke energeticheskih spektrov metodom parametricheskogo diskretnogo preobrazovaniya Fur'e (Time windows for estimating energy spectra by the method of parametric discrete Fourier transform // Avtometriya. 1983. no. 4. pp. 39 - 45.
3. Ponomarev V.A., Ponomareva O.V. Modifikaciya diskretnogo preobrazovaniya Fur'e dlya resheniya zadach interpolyacii i svertki funkcij (Modification of the discrete Fourier transform for solving problems of interpolation and convolution of functions) // Radiotekhnika i elektronika. 1984. vol. 29. no 8. pp. 1561 - 1570. 4. Ponomareva O.V. Razvitie teorii spektral'nogo analiza diskretnyh signalov na konechnyh intervalah v bazise parametricheskih eksponencial'nyh funkcij (Development of the theory of spectral analysis of discrete signals at finite intervals in the basis of parametric exponential functions) // Digital Signal Processing. 2010. no. 2. pp. 7 - 11.
5. Ponomarev V.A., Ponomareva O.V. Teoriya i primenenie parametricheskogo diskretnogo preobrazovaniya Fur'e (Theory and application of the parametric discrete Fourier transform) // Digital signal processing. 2011. no. 1. pp. 2 - 6.
6. Ponomareva O.V. Neinvariantnost' skol'zyashchego energeticheskogo parametricheskogo Fur'e-spektra dejstvitel'nyh tonal'nyh signalov (Non-invariance of the moving energy parametric Fourier spectrum of real tonal signals) // Digital signal processing. 2014. no. 2. pp. 7 - 14.
7. Ponomareva O.V. Osnovy teorii diskretnyh kosvennyh izmerenij parametrov signalov (Fundamentals of the theory of discrete indirect measurements of signal parameters). Izhevsk. Publishing house IzhSTU/ 2016. 172 p.
8. Ponomarev A.V. Dvumernaya obrabotka signalov v diskretnyh bazisah Fur'e (Two-dimensional signal processing in discrete Fourier bases) // Intellectual systems in production. 2019. vol.17. no. 1. pp.71-77.
9. Ponomareva O.V., Ponomarev A.V. Interpolyaciya v prostranstvennoj oblasti dvumernyh diskretnyh signalov s pomoshch'yu bystryh preobrazovanij Fur'e (Interpolation in the spatial domain of two-dimensional discrete signals using fast Fourier transforms) // Intellectual systems in production. 2019. vol.17. no. 1. pp.88-94.
10. Ponomareva O., Ponomarev A., Ponomarev V. Evolution of Forward and Inverse Discrete Fourier Transform // Proceedings of IEEE East-West Design & Test Symposium (EWDTS 2018). 2018. C. 313-318.
11. Ponomareva O., Ponomarev A., Ponomareva N. Window - presume Parametric Discrete Fourier Transform // Proceedings of IEEE East-West Design & Test Symposium (EWDTS 2018). 2018. C. 364-368.
12. Ponomarev V.A., Ponomareva O.V., Ponomarev A. V. Izmerenie vremennyh spektrov diskretnyh signalov na konechnyh intervalah (Measurement of time spectra of discrete signals at finite intervals) // Vestnik IzhGTU im. Kalashnikova M.T. 2016. vol.19. no2. pp. 80-83.
13. Ponomareva O.V., Alekseev V.A., Ponomarev A. V. Bystryj algoritm izmereniya spektra dejstvitel'nyh signalov metodom aperiodicheskogo diskretnogo preobrazovaniya Fur'e (Fast algorithm for measuring the spectrum of real signals by the method of aperiodic discrete Fourier transform) // Vestnik IzhGTU im. Kalashnikova M.T. 2014. no2. pp. 106-109.
14. Ponomareva O.V. Izmerenie spektrov kompleksnyh signalov na konechnyh intervalah metodom aperiodicheskogo diskretnogo preobrazovaniya Fur'e (Measurement of spectra of complex signals at finite intervals by the method of aperiodic discrete Fourier transform) // Intellectual systems in production. 2014. no. 1(23). pp.100-107.
15. Ponomarev V.A., Ponomareva O.V. Invariantnost' tekushchego energeticheskogo Fur'e–spektra kompleksnyh diskretnyh signalov na konechnyh intervalah (Invariance of the current energy Fourier spectrum of complex discrete signals at finite intervals) // Izvestiya vysshih uchebnyh zavedenij Rossii. Radioelektronika .2014. no2. pp. 8-16.
16. Rabiner L., Gold B. Theory and Application of digital signal processing. New Jersey, Prentice-hall, 1975, 772 p.
17. Gonzalez R.C., Woods R.E. Digital Image Processing, 4th Ed. Published by Pearson..–1168 (2018).
18. Pratt William K. Digital image processing. 4th edl, A Wiley-Interscience publication 2007, 807 p.
Multi-criteria synthesis for class of digital structurally protected radio signals
Kirillov S.N., e-mail: kirillov.lab@mail.ru
Lisnichuk A.A., e-mail: a.a.lisnichuk@gmail.com
The Ryazan State Radio Engineering University named after V.F. Utkin (RSREU), Russia, Ryazan
Keywords: radio signal synthesis, signal structural hiding, multi-criteria optimization, increasing noise immunity.
Abstract
To increase the noise immunity of prospective radio communication systems, a procedure has been developed for multi-criteria synthesis for class of structurally protected radio signals in order to adapt to narrow-band interference action.
To adapt prospective radio communication systems to the action of a combination of additive “white” Gaussian noise (AWGN) and other interfering factors (including narrow-band interference), it is advisable to use multi-criteria synthesis of radio signals with a dip in the power spectral density at frequencies interference action. The combined quality criterion included private criteria responsible for reducing narrow-band interference effects; noise immunity with AWGN, as well as minimizing out-of-band radiation and maximizing signal structural hiding. The application of the last criterion led in radio monitoring systems to a significant increase in the probability of bit error from detectors set of the known signals types under consideration (by up to 25%).
This, in turn, will complicate the recognition of the type of radio signal and will lead to the impossibility of unauthorized interception of the transmitted information or setting an effective (signal-like) interference. To exclude the influence of a particular modulation type recognition algo-rithm, it is advisable to consider a quality indicator that provides an increase in structural hiding in the form of maximizing the probability of a bit error from detector set of the known signals types in the case of a mixture of a synthesized signal and AWGN at a relatively high signal-to-noise ratio.
References
1. Lisnichuk A.A., “Multi-criteria synthesis procedure of DSSS signals for cognitive radio systems adaptation to complex interference environment,” Vestnik RGRTU, No. 66-1, 2018, pp. 9-15. (In Russ.).
2. Gutkin L.S., Optimizacija radiojelektronnyh ustrojstv [Optimization of radio-electronic devices] M.: Sov. radio. 1975. 368 p. (In Russ.).
3. Kirillov S.N., Lisnichuk A.A., “The multi-criteria synthesis of 16-position radio signal by signal set design for adapt data communication radio system to narrow-band interference,” Radi-otehnika – Radioengineering, No. 5, 2018, pp. 4-12. (In Russ.).
4. Kirillov S.N., Lisnichuk A.A., “Comparative analysis of the effect of narrow-band interfe-rence on cognitive radio communication systems based on synthesized four-position radio signals,” Radiotehnika – Radioengineering, No. 5, 2018, pp. 30-35. (In Russ.).
5. Lisnichuk A.A., Kirillov S.N., “Analysis of cognitive radio systems characteristics adapt-ing to narrow-band interference effect based on synthesized four-position radio signals,” Vestnik RGRTU, No. 66-1, 2018, pp. 3-8. (In Russ.).
6. Kirillov S.N., Lisnichuk A.A., “The multi-criteria synthesis of signal-code sequence based on dependent signals to adapt data communication radio system to narrow-band interference,” Vestnik RGRTU, No. 62, 2017, pp. 3-12. (In Russ.).
7. Gutkin L.S., Proektirovanie radiosistem i radioustroi`stv [Design of radio systems and ra-dio devices] M.: Radio i sviaz`, 1986. – 288 p. (In Russ.).
Resistant to recognition radio signals with controlled coupling between in-phase and quadrature components
P.S. Pokrovskij, e-mail: paulps@list.ru
The Ryazan State Radio Engineering University named after V.F. Utkin (RSREU), Russia, Ryazan
Keywords: signal recognition, classification algorithm, all-purpose radio signal former, radio signals with controlled coupling between in-phase and quadrature components, bandwidth-efficient digital modulation.
Abstract
The article deals with choosing parameters of radio signals with controlled coupling between in-phase and quadrature components (RSCCQC) to improve resistant to two known classification modulation algorithms. The RSCCQC synthesized using the combined quality index “occupied bandwidth – level of envelope fluctuation” were considered.
The preliminary analysis showed that these signals are located on the “power-bandwidth trade-off” plane in areas that is referred to both phase and frequency shift keying. At the same time the modulation type of RSCCQC retunes by changing only two parameters. The parameters define a depth of intersymbol interferences and interchannel (between in-phase and quadrature components of radio signal) interferences.
Since in practice the radio monitoring of radio signal structure is executed under condition of a prior unknown modulation type and parameters of analyzed radio signal, in this article two classification algorithms provided reliable recognition in these assumptions were selected. To evaluate the ambiguity of algorithm decisions (i.e. the resistance to recognition) the entropy is used. It was shown that the first classification algorithm has a maximum of the decision ambiguity on the set of synthesized RSCCQC at point that corresponds to a local minimum of the decision ambiguity of the second algorithm.
And so, to determine the resistant RSCCQC the combined quality index is chosen. This quality index is a weighted sum of decision entropies of the considering classification algorithms. The RSCCQC maximizing this combined criterion provides approximately equal entropy values of both algorithms. This value is 0.9 bits. It was shown that the resistant to recognition RSCCQC are comparable by basic spectral and energy characteristics with known bandwidth-efficient signals.
The work was executed with support of Russian President's Grant MK-3658.2018.9 (agreement No. 075-02-2018-681 dated 11/16/2018).
References
1. Zhuk A.P., Ivanov A.S. Povyshenie strukturnoj skrytnosti sistemy peredachi informacii s kodovym razdeleniem kanalov (Increasing the structural hiding of a communication system with code division) // Naukojomkie tehnologii v kosmicheskih issledovanijah Zemli. M., 2011. no. 1. pp. 26-28.
2. Kirillov S.N., Pokrovskij P.S. Programmno-upravljaemyj formirovatel' radiosignalov s nelinejnymi vidami moduljacii (Software-controlled shaper of non-linear modulated radio signals) // Nelinejnyj mir. M., 2013. no.3. pp. 150-157.
3. Pokrovskij P.S. Procedura sinteza radiosignalov s upravljaemoj svjaz'ju mezhdu kvadraturnymi sostavljajushhimi po dvum pokazateljam kachestva (Procedure of synthesis radio signals with controlled relationship between inphase and quadrature components by two criteria) // Vestnik Rjazanskogo gosudarstvennogo radiotehnicheskogo universiteta. Ryazan, 2015. no. 2 (issue 52). pp.49-55.
4. Prokis Dzh. Cifrovaja svjaz' (J.G. Proakis, Digital Communications). – M.: Radio i svjaz', 2000. – 800 p.
5. Makarov K.S. Metody raspoznavanija moduljacii (Methods of modulation recognition)// Cifrovaja obrabotka signalov (Digital signal processing). M., 2014, no 1. pp. 29-35.
6. O.A. Dobre, A. Abdi, Y. Bar-Ness, W. Su, “Survey of auto-matic modulation classification techniques: classical approaches and new trends,” Com. IET, vol. 1, No. 2, 2007, pp. 137–156.
7. Bhawna, M. Kaur, G.C. Lall, “Automatic Modulation Recognition for Digital Communication Signals,” IJSCE, vol. 2, 2012, pp. 110-114.
8. F. Liedtke, “Adaptive procedure for automatic modulation recognition,” Journal of Telecommunications and Information Technology, No. 4, 2004, pp. 91-97.
9. Kirillov S.N., Pokrovskij P.S. Algoritm klassifikacii vida moduljacii neizvestnogo radiosignala kosmicheskih sistem peredachi informacii (The algorithm of classification modulation type for unknown radio signal of space radio communication systems) // Vestnik RGRTU. Ryazan. 2013. no. 2, pp. 3-11.
10. Simon M.K. Bandwidth-Efficient Digital Modulation with Application to Deep-Space Communications. Jet Propulsion Laboratory. California Institute of Technology. URL: https://descanso.jpl.nasa.gov/monograph/series3/complete1.pdf
Recognition of random signals when used as features of sample characteristic functions
Parshin V.S., PhD, Dr. in technical sciences, full professor, Ryazan state radioengineering university, , e-mail: vsparshin@gmail.com
Keywords: recognition, a priori uncertainty, features, sample characteristic function, distribution moments, asymmetry and kurtosis coefficients, erroneous recognition probabilities.
Abstract
Sample characteristic functions are offered to be used as features for random signal recognition which allows us to move from the recognition in case of non-parametric a priori uncertainty to the recognition in the condition of parametric a priori uncertainty. The ratios to determine the moments of sample characteristic function distribution law allowing us to determine asymmetry and kurtosis coefficients are received. The estimation of the convergence of sample characteristic function distribution law to normal distribution is given. The comparison of probabilities for erroneous recognition of four classes of random signals using optimum algorithms and the algorithm using the values of sample characteristic function as features is carried out.
References
1. Fomin YA.A., Tarlovskij G.R. Statisticheskaya teoriya raspoznavaniya obrazov. – M.: Radio i svyaz, 1986, – 264 s.
2. Repin V. G., Tartakovskij G.P. Statisticheskij sintez pri apriornoj neopredelennosti i adaptaciya informacionnyh sistem. – M.: Sov. radio, 1977, – 432 s.
3. Fukunaga K. Vvedenie v statisticheskuyu teoriyu raspoznavaniya obrazov. Per. s angl. pod red. A.A. Dorofeyuka. – M.: Nauka, 1979, – 367 s.
4. Levin B.R. Teoreticheskie osnovy statisticheskoj radiotekhniki. – M.: Sov. radio, 1974 – 1976, kn. 1-3. – kn.1 – 552 s., kn.2 – 392 s., kn.3 – 288 s.
5. Veshkurcev YU.M. Prikladnoj analiz harakteristicheskoj funkcii sluchajnyh processov. –M.: Radio i svyaz, 2003, – 201s.
6. Parshin V.S. Ocenivanie harakteristicheskih funkcij parametrov impul'snyh sluchajnyh processov// Izv. vyssh. uchebn. zavedenij. Radioelektronika – 1989. – Ò.32. – ¹3. – S. 54-55.
7. Parshin V.S. Ocenivanie spektral'noj plotnosti moshchnosti impul'snyh sluchajnyh processov s pomoshch'yu vyborochnyh harakteristicheskih funkcij // Cifrovaya obrabotka signalov – 2016.- ¹ 4.- S. 9-13.
8. Parshin V.S., SHumilov P.A. Ispol'zovanie v kachestve priznakov dlya raspoznavaniya sluchajnyh signalov vyborochnyh harakteristicheskih funkcij. DSPA: Voprosy primeneniya cifrovoj obrabotki signalov. 2017. t.7. ¹ 3. S.26-30.
9. Koks D., L'yuis P. Statisticheskij analiz posledovatel'nosti sobytij. M.: Ìir, 1969, - 312 s.
Synthesis of Window Functions for Harmonic Analysis with Arbitrary Sidelobe Falloff Rate and Minimum Level of the Highest Sidelobe
G.V. Zaytsev, e-mail: gennady-zaytsev@yandex.ru
A.D. Khzmalyan
PJSC “Almaz R&P Corp.”
Keywords: digital signal processing, falloff rate, harmonic analysis, minimax criterion, window function.
Abstract
Application of window functions is an inherent part of digital spectral analysis algorithms. The window function is intended to mitigate the spectral leakage effect. For this purpose, the spectrum of the window must have a small main lobe width and a low sidelobe level. It is impossible to provide small values of all these parameters simultaneously; therefore, when choosing a window, it is necessary to find the most appropriate balance between the parameters from the viewpoint of the particular problem. Earlier [8-12], the authors developed families of window functions, among which the optimal values of the main lobe width and minimum level of the maximum sidelobe can be chosen on a continual basis. However, windows investigated in the literature offer only discrete values of the asymptotic spectrum sidelobe falloff rate, which are multiple of 6 decibel per octave (dB/oct).
To obtain a possibility of specifying also an arbitrary spectrum sidelobe falloff rate, it is proposed to represent the window w(t) as a product of a halfwave of the cosine function raised to the power μ (where μ is a nonnegative real number) and an initial portion of the generalized Fourier series of m+1 terms (m is a small integer, called the order of the function) in powers of the same cosine function:
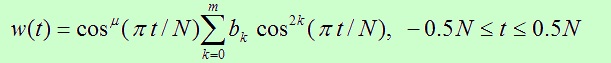
where N is the total number of sampling points over the signal duration. The first multiplier has a μth order zero at the ends of the window, which provides the spectrum sidelobe falloff rate 6(μ+1) dB/oct, that is the sidelobe falloff rate can be chosen arbitrarily.
The unknown coefficients bk of the series in the second multiplier are obtained as a solution to the minimax optimization problem so as to provide the minimum possible (at the given μ and m) maximum sidelobe level in the frequency region |f|≥β, where β is the specified main lobe halfwidth measured at the level of the highest sidelobe. It is proved that the functional of the problem is convex and the solution is unique. The problem is reduced to the linear Chebyshev approximation problem, which makes it possible to use the known mathematical theory to develop a criterion for an approximate solution obtained numerically. The criterion evaluates how close is the sidelobe level achieved to the exact minimum value. The functional is shown to have a ravine structure, and an efficient minimization method is developed. For integer μ parameters of optimal window functions are tabulated in our previous papers [8-12].
In this paper, tables of coefficients of the synthesized optimal functions and their parameters are provided for the sidelobe falloff rates 9, 15, and 21 dB/oct down to the sidelobe levels of about minus 200 dB. Simple linear relationships are obtained that give fine estimates of the equivalent noise bandwidth and minus 6-dB main lobe width of the optimum function from its minus 3-dB width. Functions are presented that feature the minimum possible level of the maximum sidelobe at m = 3, 4 and 5 and integer μ in the range from 3 through 12. Characteristics of the windows obtained are discussed and their implementation in the time and frequency domains is illustrated.
The optimal windows developed are simple to calculate and are intended for real-time applications.
References
1. F. J. Harris On the Use of Windows for Harmonic Analysis with the Discrete Fourier Transform. Proceedings of the IEEE, vol. 66, Jan. 1978, pp. 51–83.
2. V. P. Dvorkovich and A. V. Dvorkovich. Okonnye funktsii dlya garmonicheskogo analiza signalov (Window functions for harmonic signal analysis). Moscow: Tekhnosfera, 2016.
3. A. V. Oppenheim and R. V. Schafer. Discrete-Time Signal Processing, 3rd ed. Englewood Cliffs. New Jersey: Prentice-Hall, 2009.
4. W. Grobner and N. Hofreiter. Integraltafel, Teil II, Bestimmte Integrale. Wien and Innsbruck: Springer–Verlag, 1958.
5. I. S. Gradstein and I. M. Ryzhik. Tables of Integrals, Series, and Products, 7th ed. A. Jeffrey and D. Zwillinger, Eds. New York, NY: Academic, 2007.
6. A. H. Nuttall. Some Windows with Very Good Sidelobe Behavior. IEEE Trans., vol. ASSP 29, Dec. 1981, pp. 84–91.
7. Hans-Helge Albrecht. A Family of Cosine-Sum Windows for High-Resolution Measurements. Proc. Conf. ICASSP-01. Salt Lake City, 2001. N.Y.: IEEE, 2001, vol. 5, p. 3081.
8. G. V., Zaytsev. Klass vesovykh funktsii malogo poryadka dlya spectral’nogo analiza, optimal’nykh po minimaksnomu kriteriyu (A family of low-order windows for spectral analysis that are optimal by the minimax criterion). Radiotekhnika (Moscow), No. 3, 2011, pp. 21–32.
9. G.V., Zaytsev. Klass vesovykh funktsii dlya spectral’nogo analiza s vysokoi skorost’yu spada lepestkov i minimal’nym urovnem maksimal’nogo bokovogo lepestka (A family of windows for spectral analysis with high spectrum sidelobe falloff rates and minimum level of maximum sidelobe). Radiotekhnika (Moscow), No 1, 2012, pp. 55–65.
10. A. D. Khzmalyan. Novye predstavleniya vesovykh funktsii s vysokoi skorost’yu spada lepestkov spectra i minimal’nym urovnem maksimal’nogo bokovogo lepestka (Novel representations of weighting functions with high spectrum sidelobe falloff rates and the minimum level of the maximum sidelobe). Vestnik vozdushno-kosmicheskoi oborony (Moscow), No 4(20), 2018, pp. 90–100.
11. G.V. Zaytsev, A.D. Khzmalyan. A Family of Optimal Cosine-Sum Windows for Real-Time Spectral Analysis. Proc. V Int. Conf. on Engineering and Telecommunication, 2018, pp. 103-107.
12. G. V., Zaytsev and A. D. Khzmalyan. Klass optimal’nykh vesovykh funktsii dlya spektral’nogo analiza so skorost’yu spada lepestkov spectra kratnoi 12 detsibel na oktavu (A family of optimal weighting functions for spectral analysis with the spectrum sidelobe falloff rate multiple of 12 decibel per octave. Radiotekhnika i electronica (Moscow), in print.
13. L. Collatz and W. Krabs, Approximationstheorie. Tshchebyscheffsche approximation mit anwendungen. Srudgart, Germany: Teubner, 1973.
Linearly constrained adaptive space filtering algorithm and its numerically stable solution
M.V.Ratynsky, e-mail: m3v5r7@inbox.ru
A.K.Kiryakmasov , e-mail: bp19z@yandex.ru
All-Russian Scientific-Research Institute of Radio Engineering, Russian, Moscow
Keywords: adaptive space filtering, linear constraints, orthogonalization, numerical stability.
Abstract
The solution of adaptive space filtering problem for N-element antenna array is as follows:
W = R-1S, where S is array manifold vector of desired signal, R = YYH is sample estimate of input signals correlation matrix, that is obtained from input signals snapshots N x K matrix Y; (·)H stands for Hermitian conjugate. The known numerically stable solution of the problem is based on strictly equivalent presentation of inverse matrix in the form R-1 = ÔHÔ, where Ô is low triangle N x N matrix, that orthonormalizes the rows of Y (filter-orthogonalizer).
The solution of adaptive space filtering problem under L linear constraints is as follows: W = R-1C(CHR-1C)-1FH, where C is the N x L matrix of linear constraints, F is L-element row vector of linear constraints coefficients. It is shown in the article that this solution can be presented in strictly equivalent numerically stable form W = ÔÍÔCÔ1Ô1HFH, where Ô1 is upper triangular L x L matrix, that orthonormalizes the columns of the matrix Y1 = ÔÑ.
Estimation of the linearly constrained algorithm numerical stability is executed by computer si-mulation as the estimate of required computer word length for numerically stable algorithm (that uses orthogonalization) as compared with two other methods – the first based on direct matrix inversion by sequential elimination (Gauss method), and the second based on its equivalent solution of finding matrix of the form C1 = R-1C by solving the system RC1 = C.
The results obtained show that numerically stable algorithm requires lesser computer word length, the required word lengths may be different as one and a half to twice, the processing costs being comparable in all three cases.
References
1. Ratynsky M.V. Adaptation and superresolution in antenna arrays. Moscow: Radio i svyaz (Radio and communications), 2003 (in Russian).
2. Frost O.L. An algorithm for linearly constrained adaptive array processing // Proc. IEEE. 1972. V.60. No.8. P.926 – 935.
3. Applebaum S.P., Chapman D.J. Adaptive arrays with main beam constraints // IEEE Trans. Antennas and propag. 1976. V. 24. No. 5. Pp. 650 – 662.
4. Takao K., Fujita M., Nishi T. An adaptive antenna array under directional constraint // IEEE Trans. Antennas and propag. 1976. V. 24. No. 5. Pp. 662 – 669.
5. Chapman D.J. Partial adaptivity for the large array // IEEE Trans. Antennas and propag. 1976. V. 24. No. 5. Pp. 685 – 696.
6. Brandwood D.H. A complex gradient operator and its application in adaptive array theory // IEE Proc. Pts. F and H. V. 130. No. 1. Pp. 11 – 16.
7. Strang G. Linear algebra and its applications. New York, San Francisco, London: Academic Press, 1976.
8. Ratynsky M.V., Kiryakmasov A.K. Otsenka razryadnosti vichislitelnogo ustroystva, trebu-emoy dlya resheniya zadach obrabotki stokhasticheskikh signalov (Evaluation of processing word length requiredfor solving stochastic signals processing problems)// Tsifrovaya obrabotka signalov (Digital signal processing). 2016. No. 4. Pp. 40 – 42 (in Russian).
9. Van Trees H.L. Detection, estimation and modulation theory. Part IV. Optimum array processing. New York: Wiley, 2002.
10. Golub G.H., Van Loan C.F. Matrix computations. Baltimore, London: John Hopkins Uni-versity Press, 1989.
Noise stability of the modem at reception of a signal with distribution of instant values under Tikhonov's law
Yu.M. Veshkurtsev, e-mail: vym1940@mail.ru
Institute radiolektroniki, service and diagnostics (IRSID), Russia, Omsk
Keywords: dynamic chaos, statistical modulation, characteristic function, modem, demodulator, noise, noise stability, signal-to-noise ratio.
Abstract
Search of methods of reliable service, storage and information processing is conducted constantly. Information technologies on the basis of dynamic chaos and statistical modulation are already offered to consideration. Signals of systems with chaotic dynamics (chaotic signals) are equivalent to accidental processes. Therefore information technologies equally can be applied to accidental processes and to signals with moderate chaoticity, for example, to the quasidetermined signals. The transmission method of information with use of digital technology and moderate chaoticity is offered and theoretically investigated.
At the level of an invention the modem of new generation in which the method of statistical modulation based on change of characteristic function of the quasidetermined signal depending on emergence of a logical "0" and logical "1" cable signal is applied is constructed. In work Tikhonov's law is used from statistical radio engineering and on its basis the digital quasidetermined signal is constructed.
The demodulator from two independent channels is developed for reception of modulated signals with distribution under Tikhonov's law, each of which measures assessment only valid or assessment only of an imaginary part of characteristic function and compares its value to a threshold on a predefined algorithm. Qualitatively also the noise stability of both channels of the modem is quantitatively estimated during the work in the channel with "white" noise. It is shown that noise stability of both independent channels of the modem different and is, at least, two orders better than this characteristic of the known device with multiposition carrier shift and also devices with ideal phase shift keying.
References
1. Gulyaev Yu.V. Information technologies on the basis of dynamic chaos for transfer, processing, storage and information protection / Yu.V. Gulyaev, R.V. Belyaev, G.N. Vorontsov, N.N. Zologin, V.I. Kalinin, E.E. Kalyanov, V.V. Kislov, V.Ya. Kislov, V.V. Kolesov, E.A. Myasin, E.P. Chigin//Radio electronics. Nanosystems. Information technologies, 2018. Vol.10. no. 2. pp. 279 – 312.
2. Veshkurtsev Yu. M. Creation of the theory of modulation with use of the new statistical law for forming of the quasidetermined signal//Science and the World, 2019. no. 5 (69). Vol.2. pp. 17 – 26.
3. Veshkurtsev Yu.M. Way of modulation of a signal: stalemate. 2626554, Grew. Federation. No. 2016114366/5 / Veshkurtsev Yu.M., Veshkurtsev N.D., Algazin E. And; çàÿâë. 13.04.2016; îïóáë. 28.07.2017, Bulletin no. 22. 5 p.
4. Tikhonov, V.I. Statistical radio engineering. – M.: Sov. radio, 1966. 678 p.
5. Veshkurtsev Yu.M. Way of demodulation of a signal: stalemate. 2626332, Grew. Federation. No. 2016131149/27 / Veshkurtsev Yu.M., Veshkurtsev N.D., Algazin E.I.; çàÿâë. 27.07.2016; îïóáë. 26.07.2017, Bulletin no. 21. 5 p.
6. Veshkurtsev, Yu.M. Filtering in space of probabilities of additive mix of the uncentered quasidetermined signal and noise / Yu.M. Veshkurtskv, N.D. Veshkurtsev, D.A. Titov//Devices and systems. Management, control, diagnostics, 2018. no. 3. pp. 18 – 23.
7. Veshkurtsev, Yu.M. Applied analysis of characteristic function of accidental processes. – M.: Radio and communication, 2003. 204 p.
8. Vilenkin, S.Ya. Statistical processing of results of a research of random functions. – M.: Energy, 1979. 320 p.
9. The reference book on special functions / Under the editorship of M. Abramovits and I. Stigan. The lane with English Under the editorship of V.A. Ditkin and L.N. Karamzina. – M.: heads. physical edition. – mat. letters., 1979. 832 p.
10. Puzyryov P.I., Zavyalov S.A., Yerokhin V.V., Shane V.Yu. The low-speed modem for data transmission of small volume in mediumwave frequency range for the territory of the Arctic//the Omsk scientific bulletin, 2018. no. 4 (160). pp. 145 – 151.
Assessment of height of the purpose in radars of meter wave band
Pakhotin V. A., 1, e-mail: VPakhotin@kantiana.ru
Simonov R.V. 1,
Vlasova K.V. 2, e-mail: p_ksenia@mail.ru
Bessonov V.A. 1, e-mail: VBessonov@kantiana.ru
Immanuel Kant Baltic Federal University1, Russia, Kaliningrad
Kaliningrad State Technical University2, Russia, Kaliningrad
Keywords: radar-tracking systems, method of maximum likelihood, angular spectral analysis, assessment of corners of the place, purpose height.
Abstract
The problem of target altitude estimation in radar of meter wave range is considered, connected with interference of direct and reflected from ground surface by waves and with necessity to take into account phenomenon of tropospheric refraction. In the area of small angles, the directional patterns for the direct and reflected wave merge together and significantly distort estimates of the target position angles (target heights). High resolution processing techniques are required to eliminate interference errors. If the phenomenon of tropospheric refraction is not taken into account, then errors in estimating the height of the target increase significantly. The work analyzes the possibility of solving the problem of estimating the angles of place (altitude of the target) by three methods: the method of angular spectral analysis, the method based on likelihood equations, the method of maximum likelihood with high resolution, developed in the IKBFU. The results of model studies of potential capabilities of estimates of angles of place (height of target) by three methods are presented. The high resolution maximum likelihood technique has been shown to have no systematic interference errors in place angle estimates, both in the region of small correlation and in the region of large correlation of direct and reflected waves. This method together with accounting of a tropospheric refraction solves a purpose height assessment problem at ranges to distance of direct visibility at the relation signal/noise ≈ 30 dB. It has been shown that the angular spectral analysis method cannot solve this problem due to insufficient resolution. It has been shown that a method based on likelihood equations cannot solve this problem. The reason is the presence of additional (false) maxima on the surface of functional dependencies. Conclusion is given on possibility of significant increase of accuracy of target altitude estimates in modern radar of meter wave range.
References
1. Bakulev P.A. Radar-tracking systems. The textbook for higher education institutions. - M.: Radio engineering, 2004.320 pages.
2. Perov A.I. Statistical theory of radio engineering systems: manual for higher education institutions. - M.: Radio engineering, 2003.-400 pages.
3. Tikhonov V.I. Optimum signal pick-up. - M.: Radio and communication, 1983.-320 pages.
4. V.A. Pakhotin, K.V. Vlasova. Solution of a problem of definition of angular data of an object maximum likelihood method. The RGU bulletin of I. Kant. Issue 4: it is gray. physical and mathematical sciences. - Kaliningrad: RGU publishing house of I. Kant, 2010. - 173 pages.
5. Pakhotin V. A., Vlasova K.V. Bessonov V.A. Strokov V.I. Babinovich A.I. Shustov of E.I. Tekhnologiya of digital processing of simple and broadband signals on the basis of functionality of credibility. (Plenary session) Reports of the 18th International DSPA-2016 conference, series: Digital signal processing and its application. T.1, Moscow, Russia, p. 13-25.
6. Helstr K. Statistical theory of detection of signals. To.; Publishing house: M.: Foreign literature, 1963.
7. Petrov B.M. Electrodynamics and radio propagation, M.: A hot line – the Telecom, 2004. - 558 pages.
8. Military review.dfpwar.ru
9. Military review.topwar.ru
The research of the reasons of the gibbs phenomenon
Soroka E.Z., e-mail: soroka@mniti.ru
The Moscow television research institute (MNITI) 105094, Moscow, Golianovskaya ul., 7à, bld .1
Keywords: Gibbs phenomenon, spectrum, discontinuous function, smooth limiting.
Abstract
The reasons of occurrence of the Gibbs phenomenon at the spectrum cutoff of discontinuous function have been researched. Methods of decreasing and elimination of this phenomenon by smooth limiting of the spectrum of the discontinuous function have been examined.
References
1. Angot Andre. Complements de mathematique. A l’usage des ingenieurs de l’electro-technique et de telecommunications. Paris, 1957. Chap. II.
2. Max J. Methodes et techniques de traitement du signal et applications aux measures phisiques. Tome 1. Paris, New York, Masson, 1981.
3. Sergienko A.B. The digital signal processing. Sankt-Peterburg: Piter, 2002. Ch. 1 & 6.
4. Buligin V.S. Gibbs phenomenon. MFTI, the general physics department – methodical matter. URL: https://mipt.ru/education/chair/Physics/S_III/Metod_3/G_t_an/.
5. Gibbs phenomenon. URL: https://en.wikipedia.org/wiki/Gibbs_ phenomenon/
6. Ignatiev N.K. The sampling and his applications.– Moscow: Swiaz, 1980.
7. Transforms and applications handbook / editor, Alexander D. Poularikas.– 3rd ed. – Boca Raton, FL, USA: Taylor and Francis Group – 2010.
8. Harris Fredric J. On the use of windows for harmonic analysis with the Discrete Fourier Transform. Proceedings of the IEEE, vol. 66, no 1, January, 1978. P. 51- 83.
9. Davidov A.V. The weighting function. URL: http://www.geokniga.org/bookfiles/geokniga-davydovlekciipocifrovojobrabotke signalov03-effektgibbsaivesovie.pdf. 2004.
10. Dvorkovich Victor P., Dvorkovich Alexander V. Window functions for harmonic analysis of signals. Moscow. Second ed. Technosfera, 2016.
If you have any question please write: info@dspa.ru
