Abstract
The adaptation algorithms with real weights are synthesized and the relevant principles of the adaptive rejector filters (ARF) are considered. The region of the appropriate use of the ARF data determined. The analysis of the ARF efficiency conducted depending on the volume of training sample and clutter parameters.

The aim is to analyze the effectiveness of the ARF with the real weights, depending on the volume of training sample. The analysis led to the conclusion that, despite the loss filter with a complex weighting processing ARF with RWF with a priori unknown parameters clutter provides better performance than conventional maladaptive algorithms with variable weight in processing time. In the marginal efficiency gains rejection clutter data filters in comparison with the known has been installed.

On the basis of the asymptotic properties of the maximum likelihood analyzes the convergence of adaptive algorithms and the value of the loss estimates due to the limited amount of training samples, and proposed adaptive notch filter algorithms analysis method depending on the volume of training sample. The criterion of the efficiency of adaptive rejection algorithms is averaged on the basis of a statistical description of the properties of estimates of unknown parameters of clutter.

The resulting analytical expression averaged criterion establishes a connection with the suppression of clutter characteristics used estimates of parameters of clutter (interperiod correlation coefficients) and makes it relatively easy to select the volume of training sample, depending on the size of allowable loss in the filter efficiency.

Height loss with increasing filter order is due to an increase in the number of correlation coefficients to be estimated for full adaptation. Increasing the width of the spectrum interference leads to increased evaluation rms deviations and also a cause of the loss increase. These expressions allow regardless of wobble settings to choose for the ARF to the RWF arbitrary order volume of training sample on the basis of admissible losses in the marginal efficiency.

References
1. Stepanov Yu.G. Anti-Radar Camouflage (in Russian). – Мoscow: Sovetskoe Radio Publ., 1968. – 144 p.

2. Richards M.A., Scheer J.A., Holm W.A. (Eds.). Principles of Modern Radar: Basic Principles. New York: SciTech Publishing, IET, Edison. 2010. – 924 p.

3. Repin V.G., Tartakovskiy G.P. Statistical synthesis for a priori ambiguity and adaptation on information systems (in Russian) / – Мoscow: Sovetskoe Radio Publ. 1977. – 432 p.

4. Popov D.I. Optimalnaya obrabotka mnogochastotnjich signalov // Izvestiya vuzov Rossii. Radioelectronika. – 2013. – № 1. – P. 32–39.

5. Popov D.I. Adaptive rejection filter with complex weight // Vestnik Koncerna PVO «Almaz – Antej». – 2015. – № 2 (14). – pp. 21-26. (in Russian)

6. Popov D.I. Avtokompensaciya doplerovskoj fazji passivnjich pomech // Cifrovaya obrabotka signalov. – 2009. – № 2. – P. 30–33.

7. Popov D.I. Adaptivnoe podavlenie passivnjich pomech // Cifrovaya obrabotka signalov. – 2014. – № 4. – P. 32-37.

8. Popov D.I. Adaptivnije pegektornjie filtrij kaskadnogo tipa // Cifrovaya obrabotka signalov. – 2016. – № 2. – P. 53-56.

9. Gantmacher F.R. Matrix theory. M.: Nauka Publ., 1988. – 552 p.

10. Popov D.I. Analiz adaptivnjich system obnarugeniya signalov na fone passivnjich pomech // Radiotechnika. – 2016. – № 11. – P. 74-79.

Processing and coding voice signal using artifical neural networks
S.N. Kirillov, e-mail: kirillov.lab@mail.ru
E.S. Sazonova, e-mail: katrinik94@mail.ru
The Ryazan State Radio Engineering University (RSREU), Russia, Ryazan

Keywords: voice signals, algorithm of noise reduction, ITU-T Recommendation G.711, artificial neural network, perceptron, Mean Opinion Score, linear regression network, FIR filter, predictor.

Abstract
In article questions of design of primary coders of the voice signal (VS) on the basis of the artificial neural networks (ANN) are considered. This subject is very urgent as development new algorithms of processing and transmissions of VS in telecommunication systems attracts the considerable interest. In addition, the majority of VS are always in a varying degree subject to action of the acoustic noises (AN). In this regard, it is necessary to enhance algorithms of suppression of acoustic noises also.

Implementation of the adaptive to the level of acoustic noises of the coder of a source of VS with μ-companding based on an artificial neural network is offered. It was succeeded to reach lowering of level of dispersion of an acoustic noise on an output of neural network implementation of the coder of a source of the message in tens of times, on comparing with the standard codec, in case of increase in a signal-to-noise ratio from 7 to 23 dB in case of different dispersion of an acoustic noise, without lowering of subjective appraisal of quality of VS on a scale of Mean Opinion Score (MOS).

Implementation of an algorithm of a prediction of voice signals in voice coders based on ANN is offered. The analysis of a possibility of implementation of the predictor of the VS in voice coders based on ANN is carried out. Advantages of implementation of predictors based on ANN in comparison with the famous predictors based on nonrecursive FIR filters are shown. The possibility of reduction of an order of a prediction from 10% to 60% in case of the same error is proved, and lowering of an error of a prediction from 15% to 70% in case of the same order in case of implementation of predictors on the basis of ANN. Increase in subjective appraisal of quality of VS on MOS scale on 0,1-0,45 points that is essential advantage of these systems.

References
1. Gibak Kim, Phillips C Loizou. Why do speech-enhancement algorithms not improve speech intelligibility // Processing of ICASSP-2010. Vol. 1. P. 397–400.

2. Phillips C Loizou. Speech enhancement theory and practice: 1st ed. Boca Raton, FL.: CRC,2007. Releases Taylor & Francis.

3. J. Benesty, J. Chen, Y. Huang, I. Cohen Noise Reduction in Speech Processing // Springer-Verlag, 2009.

4. V. K. Zlobin, D. V. Grigorenko, V. N. Ruchkin, V. A. Romanchuk. Klusterizaciya I vosstanavlivaemost’ neyroprocessornyh sistem obrabotki dannyh (Clustering and restorability of neuroprocessor data handling systems)//Izvestiya TulGU. Tehnicheskie nauki. 2013. Issue 9. Ch.2 C. 125-133.

5. S. N. Danilin, M. V. Makarov, S. A. Shchanikov. Proyektirovanie tehnicheskih sredstv s neyrosetevoy arhitekturoy pri iskazhenii shumami vhodnoy informacii (Design of technical means with neural network architecture in case of distortion by noise of input information.) 24th Mezhdunarodnaya Krumskaya konferenciya "SVCH-tehnica I telekommunikacionnye tehnologii": materialy konf.: in 2 t. - Sevastopol, 2014.

6. Kirillov S. N., Sazonova E. S. Neyrosetevaya realizaciya predskazatelya rechevyh signalov v koderah rechi (Neural network implementation of the predictor of voice signals in voice coders)//Vestnik RGRTU No. 56 – 2016 – page 31-37

7. Kirillov S. N., Popova E. S. Neyrosetevaya realizaciya kodera rechevyh signalov adaptivnogo k urovn’u akusticheskih shumov (Neural network implementation of the coder of voice signals of the adaptive to the level of acoustic noises). Vestnik RGRTU, 2015 No. 54, page 40-44

8. Bolodurina, V. N. Reshetnikov, M. G. Taspayeva. Primeneniya i adaptaciya neyrosetevyh technologiy v zadache identifikacii dinamicheskih obyektov (Application and adaptation of neural network technologies in the task of identification of dynamic objects.) Programmnye produkty, sistemy i algoritmy No. 1, 2012 of.

9. Ciresan D., Meier U., Masci J and Schmidhuber J. Multi-column Deep Neural Network for Traffic Sign Classification. Neural Networks, Vol. 34, August 2012, pp. 333 – 338И.П.

10. O. E. Karasyov Primenenie teorii nechetkih mnozhestv dlya obrabotki videoinformacii v telekommunikacionnyh sistemah (Applycation of the theory of indistinct sets for processing of video information in telecommunication systems.) VI Vserossiyskie nauchnye Zvorykinskie chteniya: sb.tez.dokl. Vserossiyskoy mezhvuzovskoy nauchnoy konferencii. Murom: Izd. - polygraphicheskiy center MI VLGU, 2014. - 791 pages.

11. Eremin D. M., Gartseev I. B. Iskusstvennye neyronnye seti v intelektual’nyh sistemah upravleniya (Artificial neural networks in intellectual management systems.) — M.: MIREA, 2004. — 75 pages.

12. Yasnitsky L. N. Vvedenie v iskusstvennyy intellect (Introduction to an artificial intelligence.) — M.: Izdat. center "Academiya", 2005. — 176 pages — ISBN 5-7695-1958-4.

13. Martinetz M., Berkovich S., Schulten К. “Neural-gas” network for vector quantization and its application to time scries prediction H Trans. Neural Networks, 1993.- Vol. 4.

14. Gill P. Murray W., Wright M. Practical Optimization. - N.Y.: Academic Press, 1987.

15. J. Sohn, N. S. Kim, and W. Sung. A statistical model-based voice activity detection. IEEE Signal Processing Lett., 6 (1): 1–3, 1999.

16. Ephraim, Y. & Malah, D. Speech enhancement using a minimum-mean square error short-time spectral amplitude estimator IEEE Trans Acoustics Speech and Signal Processing, 32(6):1109-1121, Dec 1984

17. Rainer Martin. Noise power spectral density estimation based on optimal smoothing and minimum statistics. IEEE Trans. Speech and Audio Processing, 9(5):504-512, July 2001.

18. Rekomendatsiya MSE-TP.80/P.800

19. GOST P 51061-97 Sistemy nizkorostnoy peredachi rechi po cifrovym kanalam. Parametry kachestva rechi I metody izmereniy (System of low-speed transmission of the speech on digital links. Parameters of voice quality and methods of measurements. )– Vved. 01.01.98. – M.: Gosstandart Rossii

20. Strogonov A. Ispol’zovanie neyronnyh setey dlya prognozirovania degradacii vyhodnyh parametrov TTL IS v sistemah MATLAB/Simulink/ (Use of neural networks for prediction of degradation of the TTL ICs output parameters in the MATLAB/Simulink system)//Componenty i tehnologii. No. 1. 2006.

21. Deacons V. P., Abramenkov I. V., Kruglov V. V. MATLAB 5.3.1. s paketami rashireniy (MATLAB 5.3.1 with packets of extensions.) M.: Nolidzh. 2001

About new stage of optimizing coding theory developing
Zolotarev V.V., e-mail: zolotasd@yandex.ru
The Ryazan State Radio Engineering University (RSREU), Russia, Ryazan Space Research Institute of RAS, Russia, Moscow

Keywords: communication systems, data storage systems, error-correction coding, computer simulation, self-orthogonal codes, concatenated codes, multithreshold decoders, coding gain, communication channel.

Abstract
The results obtained during the 25-year evolution of the error-correction coding optimization theory (OT) and multithreshold decoding (MTD) methods, which have been created on its basis, are presented. It is shown the MTD provides near to optimal performance even for channels with high noise level. Wherein the complexity of MTD is linear on code length only.

The performance analysis for binary MTDs over Gaussian channel is fulfilled in this paper. It is shown best MTDs can provide coding gain comparable or better than coding gain for known practical implemented error-correction methods as Viterbi decoder for short convolutional codes, decoders for turbo and low-density parity-check codes.

The symbolic error-correction codes over q-ary symmetric channel are discussed. It is shown the symbolic MTDs (qMTDs) solve fully all problems for digital world in transmission, storage and recovering digital data in any information system. The qMTDs are many times better than decoders for Reed-Solomon (RS) codes in error correction and implementation complexity. It allows to claim the qMTDs can replace RS codes in any applications.

In the paper it is shown the MTD algorithms have also no concurrent in complexity and performance over erasure channels.

The methods, properties and possibilities of codes and algorithms allowing improve the MTD and qMTD performance in a simple way and forming very powerful perspective intellectual space for de-coding methods developing are discussed additionally. These new paradigms of OT have allowed to create methods for different coding clusters working effectively near to channel capacity. The development of these methods transfer to new code structure rapidly.

The results presented testify successful decision of main scientific and technological problems for our informational digital civilization – developing of simple methods for achievement of high reliable transmission, storage and recovering for digital information. Solution of these complex problems allows to switch efforts of engineers and scientists for solve new important tasks for our digital world.

References
1. Zolotarev V.V., Suboptimal'nye algoritmy mnogoporogovogo dekodirovaniya: dis. d-ra tekhn. nauk (Suboptimal multithreshold decoding algorithms: Doct. tech. sci. thesis), Moscow, 1990. 278 p.

2. Zolotarev V.V. Teoriya i algoritmy mnogoporogovogo dekodirovaniya (Theory and algorithms for multithreshold decoding). Moscow: Radio i svyaz', Goryachaya liniya – Telekom, 2006, second edition - 2014.

3. Zolotarev V.V., Zubarev Yu.B., Ovechkin G.V. Mnogoporogovye dekodery i optimizatsionnaya teoriya kodirovaniya (Multithreshold decoding and optimizing coding theory). Moscow: Goryachaya liniya – Telekom, 2012. 238 p.

4. Zolotarev V., Zubarev Y., Ovechkin G. Optimization Coding Theory and Multithreshold Algorithms. Geneva, ITU, 2015, 159 p.

5. Zolotarev V.V., Ovechkin G.V. Primenenie mnogoporogovykh metodov dekodirovaniya pomekhoustoichivykh kodov v vysokoskorostnykh sistemakh peredachi dannykh, Elektrosvyaz'. Moscow, 2014, No. 12, P. 10-14

6. Kuznetsov N.A., Zolotarev V.V., Ovechkin G.V., Ovechkin P.V. Nedvoichnye mnogoporogovye dekodery i drugie metody korrektsii oshibok v simvol'noi informatsii, Radiotekhnika. Moscow, 2010, No.6, Issue 141, P. 4-9.

7. Zolotarev V.V., Ovechkin G.V., O sopostavlenii novykh metodov pomekhoustoichivogo kodirovaniya, Proc. of 18-th Int. Conf. "Digital Signal Processing and Its Applications". Moscow, 2016, P. 59–65.

8. Massey J., Threshold decoding, Cambridge, Massachusetts: M.I.T. Press, 1963.

9. Clark G., Jr., Cain B. Error-Correction Coding for Digital Communications. New York: Plenum Press, 1981.

10. Zolotarev V.V., Nazirov R.R., Nikiforov A.V., Chulkov I.V. Novye vozmozhnosti mnogoporogovogo dekodirovaniya po vysokodostovernoi peredache dannykh DZZ, Sovremennye problemy distantsionnogo zondirovaniya zemli iz kosmosa. Sbornik nauchnykh statei. Moscow, OOO "Azbuka-2000", 2009, Issue 6, Vol. I. P. 167-173.

11. Zolotarev V.V., Nazirov R.R., Chulkov I.V., Ovechkin G.V. Algoritmy MPD, Rossiiskii kosmos. Moscow, 2009, No. 1, P. 60–63.

12. Zolotarev V.V., Ovechkin G.V., Nazirov R.R., Ovechkin P.V., Chulkov I.V. Effektivnoe nedvoichnoe mnogoporogovoe dekodirovanie pomekhoustoichivykh kodov dlya sistem distantsionnogo zondirovaniya Zemli, Sovremennye problemy distantsionnogo zondirovaniya Zemli iz kosmosa, Sbornik statei. Moscow, 2010, Vol. 7, No. 2, P. 269-274.

13. Zolotarev V.V., Chulkov I.V. Maloizbytochnoe kodirovanie dlya vysokoskorostnykh kanalov, Proc. of 11-th Russian open conf. "Sovremennye problemy distantsionnogo zondirovaniya Zemli iz kosmosa". Moscow, 2013.

14. Ovechkin G.V., Teoriya kaskadnogo dekodirovaniya lineinykh kodov dlya tsifrovykh radiokanalov na osnove mnogoporogovykh algoritmov: dis. d-ra tekhn. nauk (Theory of concatenated de-coding of linear codes based on multithreshold algorithms for digital radiochannels: Doct. tech. sci. thesis). Ryazan, 2011, 301 p.

15. Ovechkin P.V. Razrabotka algoritmov povysheniya effektivnosti nedvoichnykh mnogoporogovykh dekoderov v sistemakh peredachi i khraneniya bol'shikh ob"emov informatsii: dis. kand. tekhn. nauk (Development of algorithms for improving performance of symbolic multithreshold decod-ers in high volume data transmission and storage systems: Cand. tech. sci. thesis). Ryazan, 2009, 131 p.

16. Zolotarev V.V., Ovechkin G.V., Satybaldina D.Zh., Tashatov N.N., Adamova A.D. Sposob myagkogo mnogoporogovogo dekodirovaniya pomekhoustoichivogo koda. Patent Kazakhstan Respublic 93989. Priority date 15.10.2014.

17. Zolotarev V.V., Ovechkin P.V. Sposob kodirovaniya i dekodirovaniya blokovogo koda s ispol'zovaniem algoritma Viterbi. Patent RF 2608872, Priority date 25.01.2017.

18. Zolotarev V.V., Ovechkin G.V. Sposob raboty simvol'nogo porogovogo elementa v simvol'nom mazhoritarnom dekodere. Patent RF 2573741. Priority date 22.12.2015.

19. Zolotarev V.V. Sposob dekodirovaniya pomekhoustoichivogo koda. Patent RF 2557454. Priority date 25.06.2015.

20. Zolotarev V.V., Ovechkin G.V. Ustroistvo mnogoporogovogo dekodirovaniya lineinykh kodov dlya gaussovskikh kanalov. Patent RF 44215. Priority date 27.02.2005.

21. Zolotarev V.V. Vysokoskorostnoe ustroistvo mnogoporogovogo dekodirovaniya lineinykh kodov. Patent RF 44216. Priority date 27.02.2005.

22. Zolotarev V.V., Averin S.V. Non-Binary Multithreshold Decoders with Almost Optimal Performance, Proc. of 9-th ISCTA’07. UK, Ambleside, 2007.

23. Averin S.V., Ovechkin G.V., Zolotarev V.V. Algorithm of Multithreshold Decoding for Self-Orthogonal Codes over Gaussian Channels, Proc. of 11-th ISCTA’09. UK, Ambleside, 2009.

24. Zolotarev V.V., Ovechkin G.V., Divergentnoe kodirovanie svertochnykh kodov, Proc. of 13th Int. Conf. "Problemy peredachi i obrabotki informatsii v setyakh i sistemakh telekommunikatsii". Ryazan, 2015, P. 27–32.

25. Zolotarev V.V. Ustroistvo dlya dekodirovaniya lineinykh svertochnykh kodov. Patent USSR 492878. Priority date 31.07.1972.

26. Samoilenko S.I., Davydov A.A., Zolotarev V.V., Tret'yakova E.L. Vy-chislitel'nye seti (Computing networks). Moscow: Nauka, 1981, 278 p.

27. Strekalovskii A.S. Individual message, 2016.

28. Zolotarev V.V. Sposob dekodirovaniya pomekhoustoichivogo koda. Patent RF 2377722. Priority date 27.12.2009.

29. Web sites www.mtdbest.ru and www.mtdbest.iki.rssi.ru.

30. Zolotarev V.V. Mnogoporogovoe dekodirovanie v stirayushchikh kanalakh, Voprosy radioelektroniki. Seriya EVT. Moscow, 1983, Issue 10, P. 67-70.

31. Grinchenko N.N., Zolotarev V.V., Ovechkin G.V., Ovechkin P.V. Primenenie mnogoporogovogo dekodera v kanalakh so stiraniyami, Trudy NTORES im. A.S. Popova. Moscow, 2006. P. 338-340.

32. Zolotarev V.V., Ovechkin G.V., Fediov V.S. Povyshenie dostovernosti khraneniya tsifrovykh dannykh na flesh-pamyati, Proc. of 6-th Int. Conf. "Kosmonavtika. Radioelektronika. Geoinformatika". Ryazan, 2013, P. 201–203.

33. Ovechkin G.V., Kao V.T. Mnogoporogovye dekodery dlya gaussovskikh kanalov, Proc. of 19-th Russian sci.-tech. conf. "Novye informatsionnye tekhnologii v nauchnykh issledovaniyakh i v obrazovanii". Ryazan, RGRTU, 2014, P. 121-122.

34. Grinchenko N.N., Kao V.T., Ovechkin G.V. Povyshenie effektivnosti mnogoporogovogo dekodera, Proc. of 17-th Int. conf "Tsifrovaya obrabotka signalov i ee primenenie – DSPA 2015". Moscow, 2015.

35. Zolotarev V., Ovechkin G., Satybaldina D., Tashatov N., Adamova A., Mishin V. Effective multithreshold decoder for optical and other data transmission systems, Proc. of 18-th Int. Conference on Communications (part of CSCC’14). Santorini Island, Greece, 2014, P. 152-156.

36. Zolotarev V., Ovechkin G., Satybaldina D., Tashatov N., Adamova A., Mishin V. Efficiency multithreshold decoders for self-orthogonal block codes for optical channels, International Journal of Circuits, Systems and Signal Processing. 2014, Vol. 8. P. 487-495.

37. Sudan M. Decoding of Reed Solomon codes beyond the error-correction bound, Journal of Complexity. 1997, Vol. 13, P. 180-193.

38. Zolotarev V.V., Ovechkin G.V. Pomekhoustoichivoe kodirovanie. Metody i algoritmy. Spravochnik (Error-correcting coding. Methods and algorithms. Handbook). Moscow: Goryachaya liniya – Telekom, 2004, 126 p.

39. Zolotarev V.V., Mnogoporogovoe dekodirovanie v nedvoichnykh kanalakh, Voprosy radioelektroniki, seriya EVT. Moscow, 1984, Vol. 12. P. 73-76.

40. Zolotarev V.V. Algoritmy korrektsii simvol'nykh dannykh v vychislitel'nykh setyakh, "Voprosy kibernetiki", VK-105, AN SSSR, Nauchnyi sovet po kompleksnoi probleme "Kibernetika". Mos-cow, 1985, P. 54-62.

41. Blokh E.L., Zyablov V.V. Obobshchennye kaskadnye kody (Generalized concatenated codes). Moscow: Svyaz', 1976.

42. Zolotarev V.V., Ovechkin G.V., Tashatov N.N. Primenenie printsipa divergentsii pri dekodirovanii svertochnykh kodov, Proc. of 3-th Int. sci.-pract. conf. "Informatsionnaya bezopasnost' v svete Strategii Kazakhstan-2050". 2015, P. 158-164.

43. Zolotarev V.V., Nazirov R.R. Blokovaya modifikatsiya algoritma Viterbi, Proc. of 11th Russian Conf. "Sovremennye problemy distantsionnogo zondirovaniya Zemli iz kosmosa". Moscow, 2013.

44. Zolotarev V.V., Ovechkin P.V. Kharakteristiki dekodirovaniya blokovykh kodov po algoritmu Viterbi dlya sistem DZZ, Proc. of 13-th Russian open conf. "Sovremennye problemy distantsion-nogo zondirovaniya Zemli iz kosmosa". Moscow, 2015.

45. Arikan E. Channel Polarization: A Method for Constructing Capacity-Achieving Codes for Symmetric Binary-Input Memoryless Channels, IEEE Transactions on Information Theory. 2009, Vol. 55, No. 7, P. 3051-3073.

46. Ovechkin G.V., Chikin A.V. Pomekhoustoichivost' priemnika sputnikovykh signalov DVB-S2, Proc. of 11-th Int. Conf. "Digital Signal Processing and Its Applications". Moscow, 2009, P. 578–580.

47. Zubarev Yu.B., Zolotarev V.V., Ovechkin G.V., Ovechkin P.V. Optimizatsionnaya teoriya kodirovaniya: itogi 25 let razvitiya, Proc. of 18-th Int. conf. "Tsifrovaya obrabotka signalov i ee primenenie – DSPA 2016". Moscow, 2016, Vol. 1, P. 6-12.

48. Kudryashov B.D. Osnovy teorii kodirovaniya (Bases of coding theory). Saint-Petersburg.: BKhV-Sankt-Peterburg, 2016, 393 p.

49. Zolotarev V.V. Primenenie divergentnogo kodirovaniya v kanalakh sputnikovoi svyazi i DZZ, Proc. of 13-th Russian open conf. "Sovremennye problemy distantsionnogo zondirovaniya Zemli iz kosmosa". Moscow, 2015. 50. Zubarev Yu.B., Zolotarev V.V., Ovechkin G.V., Ovechkin P.V. Itogi 25-letnego razvitiya optimizatsionnoi teorii kodirovaniya, Naukoemkie tekhnologii. Moscow, 2016, Vol. 17, P. 26-32.

51 Zolotarev V.V. Mnogoporogovoe dekodirovanie, Problemy peredachi informatsii. Moscow, 1986, Vol. 11, Issue 1, P. 104-109.

52. Zolotarev V.V., Ovechkin G.V., Ovechkin P.V. Blokovaya modifikatsiya algoritma Viterbi, Vestnik RGRTU. Ryazan, 2017, No. 59, P. 30-35.

53. Zolotarev V.V., Ovechkin G.V., Barinov I.V. Primenenie samoortogonal'nykh kodov v kaskadnykh skhemakh kodirovaniya dlya kanalov svyazi so stiraniyami, Proc. of 19-th Int. conf. "Tsifrovaya obrabotka signalov i ee primenenie – DSPA 2017". Moscow, 2017, Vol. 1, P. 59-63.

54. Zolotarev V.V. Sposob obnaruzheniya i ispravleniya stiranii pri prieme diskretnoi informatsii. Patent RF 2611235. Priority date 21.02.2017.

Dynamic characteristics parametric models and filters in the frequency domain
V.I. Koshelev, PhD (technical sciences), full professor, Head of the Department, e-mail: koshelev.v.i@rsreu.ru
The Ryazan State Radio Engineering University (RSREU), Russia, Ryazan

Keywords: dynamic frequency characteristics of filters, shortening of transient processes duration.

Abstract
We consider the problem of analyzing the frequency characteristics of the filters with incomplete transient(dynamic frequency characteristics). Such tasks are characteristic for the IIR filters, including those based on autoregressive models, and for FIR-filters, in particular moving average filters. A particularly important application of the presented approach is for cascade filters. We analyze the methods of reducing the duration of transients to improve the dynamic frequency characteristics of the filters. The aim of this work is to analyze the extent to which the static and dynamic frequency characteristics of the filters depend on the length of the sample and to develop methods for acceleration of transients in IIR filters.

The article analyzes the methods of calculating the frequency characteristics of the filter for uncompleted transient processes. It is shown that the known methods for calculating the dynamic frequency characteristics of IIR filters in unsteady (transient) mode with increasing sample size yield results that are close in terms of the mean square error, but they differ significantly by the criterion of the maximum deviation. In general, the proposed method with an equivalent length of the sequence leads to smaller errors, and the frequency response is closer to the static characteristic. The initialization method allows to bring the dynamic frequency characteristics closer to static ones and substantially shorten the duration of transient processes in the filter.

References
1. S.Lawrence Marple, Jr. Digital Spectral Analysis with Applications: Prentice-Hall, Inc., Englewood Cliffs, New Jersey 07632.: 1987.– 584 p.

2. Fletcher-ml., Burleigh D. Metod predvaritelnoy obrabotki signalov dlj uluchschenia raboty ustroistva selekziy dvigugihsj zelei v radiolokatorash s FAR //TIIER. 1972.– №12.– C. 137 138.

3. Koshelev V.I. ARSS modeli sluchainysh processov. Prikladnye zadachi sinteza i optimisazii. M.: Radio i svjas, 2002. 116 s.

4. Vitajzev V.V. Mnogoskorostnaj obrabotka signalov. M.: Gorjachaja liniaj telecom, 2017. 336s.

5. Koshelev V.I., Andreev V.G. Optimizaziaj avtoregressionych modeley processov s polimodalnym spektrom/ Izvestia vuzov. Radioelectronika. 1996. Т. 39. № 5. s. 43-48.

6. Koshelev V.I. Ozenka kachestva modelej sluchainych processov pri korotkoj vyborke //Vestnic RGRTA. Ryazan. 2001, Vyp 8. s. 31-35.

7. Koshelev V.I., Andreev V.G. Adaptivnaj obrabotka signalov v filtrach s perestraivaemymi porjdkami //SVCh-technica i sputnicovy priem: Materialy 3-ei Crymskoi conferenzii: V 6-ti t., g. Sevastopol, 20-23 sentajbraj 1993 g. Sevastopol: ECOSI Gidrofizika, 1993 – T.3 s. 285-287.

8. Director S., Rohrer R. Vvedenie v teoriu system: Per. s angl. ped N.P. Buslenko. – M.: Mir, 1974. – 464 s.

Statistical approach to design and analysis of detection algorithms of fractal signals and fractal images
Parshin A. Yu, e-mail: parshin.a.y@rsreu.ru
Parshin Yu. N., e-mail: parshin.y.n@rsreu.ru
The Ryazan State Radio Engineering University (RSREU), Russia, Ryazan

Keywords: correlation dimension, optimal estimation, maximum likelihood estimation, fractal Brownian motion, error probability of edge detection.

Abstract
The paper deals with the development of algorithms for processing of fractal signals and images. The investigated processes are not considered as a simple set of separate elements with certain characteristics, but as a structure with internal topological connections between the elements. A distinctive property of such structures is the non-integer nature of their dimension, which characterizes the general property of self-similarity.

Description and analysis of the parameters of fractal phenomena are considered in context of the theory of optimal statistical solutions. A statistical interpretation of the correlation integral is used, as the probability of a non-exceeding of a given scale value by distances between vectors formed by signal or image samples in a pseudo-phase space. The correlation dimension is chosen as a fractal measure of signals and images. The algorithms for object and edge detection on the image are obtained by maximum likelihood method.

When solving the task of detecting objects on images, the methods of texture analysis are used, where the correlation dimension is chosen as the texture property. The fractal image is given in the form of a two-dimensional fractal Brownian motion - a fractal Brownian surface, as well as a set of distances between vectors in a pseudo-phase space. A refinement of the description of the distances between vectors in a pseudophase space with considering of their given topological dependence, and their probabilistic description is proposed.

Expressions for the likelihood ratio logarithm are obtained, the error probabilities are calculated for the object and edge detection in case of Gaussian and non-Gaussian approximations. It is shown that the maximum likelihood estimate of the correlation dimension is sufficient statistics for the detection problem. It is proposed to determine the quality of the edge detection by a system of error probabilities - the probability of false edge fields and the probability of skipping the edge.

Algorithm of correlation dimension estimation is modified for case of depended distances between vectors. Geometrical dependence affects the value of dimension estimate. It is shown, that proposed algorithms are effective for correlation dimension estimation due to large amount of data, obtained from radar with synthesized aperture of antenna. Despite of high computational complexity of fractal dimension estimation it is possible to simplify computational process by usage of statistical description.

References
1. A.A. Potapov, Fractals in Radio Physics and Radiolocation: Selection Topology. Мoscow: Universitetskaya kniga, 2005.

2. Culter C.D. A Review of the Theory and Estimation of Fractal Dimension // Nonlinear Time Series and Chaos. V.1. Dimension Estimation and Models, 1993. P. 1-107.

3. Parker T.S., Chua L.O. Chaos: A Tutorial for Engineers // Proceedings of the IEEE, 1987, T. 75, № 8. С. 982-1008.

4. Sosulin Yu.G. Theory of Detection and Estimation of Stochastic Signals. M.: Sovetskoe radio, 1978. 320 p.

5. Sosulin Yu.G., Parshin Yu.N. Estimating-Correlation-Compensating Processing of Multidimensional Signals // Radiotechnica i electronica. 1981. V..26, №8. pp. 1635-1643.

6. Sosulin Yu.G., Kostrov V.V., Parshin Yu.N. Estimating-Correlation Processing of Signals and Interference Compensation. M.: Radiotechnica, 2014. 632 p.

7. R.M. Crownover. Introduction to Fractals and Chaos. Jones and Bartlett, 1995.

8. Pisarenko D. V., Pisarenko V.F. Statistical Estimation of the Correlation Dimension // Physics Letters, A b(197), 1995. P.31-39.

9. Luca L., Lasocki S., Luzio D., Vitale M. Fractal Dimension Confidence Interval Estimation of Epicentral Distribution // Annali di Geofisica, 42(5), 1999. P.911-925

10. Luciana De Luca, Dario Luzio, Massimo Vitale. A ML Estimator of the Correlation Dimension for Left-Hand Truncated Data Samples // Pure and Applied Geophysics, V.159, № 11-12, 2002. P. 2789-2803.

11. Parshin A.Yu., Parshin Yu.N. Complexing of Energy and Fractal Detectors // Problems of transmission and processing of information in telecommunications networks and systems. 17-th International scientific and technical conference. Part 2. Ryazan: RSREU, 2012. P. 37-39.

12. Parshin A., Parshin Yu. Usage of non-Gaussian Statistics for RF Signals Detection by Complex Energy and Fractal Detector // International Radar Symposium - IRS 2013, Proceeding, volume I, II, Drezden, Germany. – German Institute of Navigation, 2013, pp. 779-784.

13. Parshin A., Parshin Yu. Using the Maximum Likelihood Estimates of Fractal Dimension in non-Gaussian Statistics for Detecting Radio Signals // Digital Signal Processing. 2013. №1. p. 42-46.

14. Parshin A.Yu., Parshin Yu.N. Synthesis and Analysis of Efficiency of Algorithm for Objects Edges Detection by Maximum Likelihood Method // 2nd Mediterranean Conference on Embedded Computing (MECO). Budva. Montenegro. June 15th-21st 2013. 282 p.

15. Sosulin Yu.G., Russkin A.B. Fractal Detection of Extensive Low in Contrast Objects on Images // Radiotechnica. 2009. № 12. P. 48-57.

16. Pesin Ya. B. On Rigorous Mathematical Definitions of Correlation Dimension and Generalized Spectrum for Dimensions // Journal of Statistical Physics, V.71, 1993. P.529-547.

17. Grassberger P., Procaccia I. Characterization of Strange Attractors // Physical Review Letters, V.50, 1983. P.346-349.

18. Packard N.H., Crutchfield J.P., Farmer J.D, Shaw R.S. Geometry from a Time Series // Physical Review Letters, V.45, 1980. P.712-716.

19. Takens F. Detecting Strange Attractors in Turbulence // Lecture Notes in Mathematics, V. 898, 1981. P. 366-381.

20. Ying-Cheng Lai, David Lerner. Effective Scaling Regime for Computing the Correlation Dimension from Chaotic Time Series // Physica D, V.115, 1998. P.1-18.

21. Antipov O.I., Neganov V.A., Potapov A.A. Deterministic Chaos and Fractals in Discrete-Nonlinear Systems. M.: Radiotechnica, 2009. 235 p.

22. Cees Diks. Nonlinear Time Series Analysis: Methods And Applications (Nonlinear Time Series and Chaos: v.4) World Scientific. 1999. 209 p.

23. Theiler J. Spurious Dimensions from Correlation Algorithms Applied to Limited Time-series Data // Physical Review. A 34. 1986. pp. 2427-2432.

24. Fried E., Absztrakt Algebra, Elemi Uton. Budapest, Muszaki Konyvkiado, 1972. 260 p.

25. Provenzale A., Smith J.A., Vio R., Murate G. Distinguishing Between Low-Dimensional Dynamics and Randomness in Measured Time Series // Physica D 58. 31-49. 1992.

26. Shuster G. Determined chaos: Introduction. M.: Mir. 1988. 240 p.

27. Parshin A.Yu., Parshin Yu.N. The Maximum Likelihood Estimation of the Correlation Dimension, Taking into Account the Influence of the Estimation Bias and Truncation of the Range of Scales // Bulletin of Ryazan State Radioengineering University. 2013. №4-1 (46.). P.18-25.

28. Hong Qian, Gary M Raymond, James B Bassingthwaighte. On Two-Dimensional Fractional Brownian Motion and Fractional Brownian Random Field // Journal of Physics A: Mathematical and General, V.31, No. 28 (1998) P. L527-L535.

LLR Calculation for OFDM signal using constellation rotation technique
A. S. Levchenko, e-mail: levch.andrew@gmail.com
National Research University «Moscow Power Engineering Institute»

Keywords: COFDM, soft demodulator, log-likelihood ratio, VHF band, RAVIS, rotated constellation, constellation rotation.

Abstract
Method that allows to specify log-likelihood ratio for OFDM signal using DVB-T2’s constellation rotation technique is proposed in the paper.

When OFDM signal is propagated through multipath channel, estimation of channel parameters is necessary for its demodulation. Even the best estimation methods have a non-zero error. As a result, bits which are transmitted through the multipath channel by constellation points with higher amplitude and all other things being equal, have lower reliability. Proposed method allows to specify log-likelihood ratio for OFDM signal with constellation rotation technique by taking into account multiplicative noise component of signal caused by estimation of channel parameters. Unlike the common method, in the proposed method I and Q components are not considered as one-dimension modulated, but method still have low computational complexity.

Results of competitive modeling using terrestrial broadcasting system RAVIS model in DRM+ multipath propagation channel models are listed for cases when constellation rotation technique is used and without it. SNR advantage of using proposed demodulation method is determined. Modeling shows that for QPSK constellation SNR advantage is more than 1 dB with coderate ¾, in range from 0.2 to 0.5 with coderate ½. For 16-QAM constellation SNR advantage is more than 0.3 dB with coderate ¾, with coderate ½ there is no SNR advantage.

Thus, using of constellation rotation technique makes sense with high data rate and low constellation order and can be achieved without significant calculation complexity increase.

References
1. ETSI EN 302 755: «Digital Video Broadcasting (DVB); Frame structure channel coding and modulation for a second generation digital terrestrial television broadcasting system (DVB-T2)», 2014.

2. GOST R 54309-2011. Real-time Audio Visual Information System (RAVIS). Process of frame structure generation, channel coding and modulation of digital terrestrial narrowband broadcasting VHF-band system. Technical specifications.

3. ETSI TS 102 831: «Digital Video Broadcasting (DVB); Implementation guidelines for a second generation digital terrestrial television broadcasting system (DVB-T2)», 2012.

4. Levchenko A. S. Demodulator COFDM signala s multiplicativnimi schumami // Radiotechnicheskie i telecommunikacionnie sistemi. №1, 2016.

5. ETSI ES 201 980 V3.1.1 (2009-08). Digital Radio Mondiale (DRM); System Specification.

Characterization of mismatched filtering method, minimizing integrated sidelobe level for phase-coded pulse
G.V. Zaytsev., e-mail: gennady-zaytsev@yandex.ru
N.S. Kondranina., e-mail: kondranina.nataliya@gmail.com
D.M. Litvinov, e-mail: litvinov_dmitry@inbox.ru
PSC SIC "Almaz"

Keywords: phase-coded pulse, mismatched filtering, minimization of integrated sidelobe level.

Abstract
Sidelobe suppression of a phase-coded radar pulse at the receiver filter output is a classical problem which also arises in many other technical domains. Search for optimal solution of this problem may be often accomplished only by exhaustive search. In a special case of minimizing integrated sidelobe level (ISL) for a fixed modulation sequence the problem may be solved analytically [5] although resulting performance is not described in the literature. The paper investigates filter output characteristics which may be achieved using this method for a binary modulation sequences and a zero Doppler shift.

Let s₀ be the modulation binary sequence, expressed by row vector, with n elements ±1, let s denote the sequence of length N containing s₀ as a central part with m proceeding and m subsequent zeros, and let x be a real row vector of the filter pulse response. Filter output is a crosscorrelation function of sequences x and s :
,
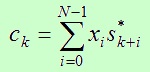where k is the index of nonzero output sample:
.
Integrated sidelobe level is determined by expression

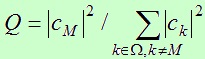
and calculated in decibels, where M is the index of the main lobe. It is shown in the paper, following [5], that optimal vector x minimizing ISL for a fixed s, is given by the formula
x = sR^-1, where R is a certain N×N matrix, which is a function of s.

The paper investigates properties of filter output for this solution. Several families of modulation sequences are considered: M sequences, Legendre sequences, and sequences up to length 271 with best known integrated sidelobe level of autocorrelation function (best-ACF family). For each sequence family main characteristics of the filter output are calculated and analyzed: integrated sidelobe level, peak sidelobe level (PSL), loss in signal-to-noise ratio in comparison with matched filer.

For best-ACF family roughly half of the sequences demonstrates approximately linear growth in decibels of the quality criterion Q(m/n), the slope of the function being 8 16 dB for each unity step of the ratio m/n. Loss in signal-to-noise ratio for these sequences is rather low, about 0.5-1.5 dB for m≤2n. Sequences with slope greater than 14 dB are tabulated in the paper.

Main characteristics for Legendre sequences are somewhat worse but they may be used for arbitrary large , where best-ACF sequences are not known. M-sequences have poor parameters so they are not recommended for use in the method considered. Average values for characteristics mentioned above are tabulated in the paper for all three sequence families.

Thus extending the length of the filter response up to (3 - 5)n leads to increasing ISL up to 25-45 dB and PSL up to 45-60 dB for large amount of sequences, keeping the loss in signal-to-noise ratio less than 1 dB. So mismatched filtering minimizing ISL is a useful method applicable not only to short-length sequences but (despite common opinion) to long sequences as well. Modern signal processors enable straightforward implementation of the discussed mismatched filtering in real time.

References
1. N. Levanon, E. Mozeson. Radar Signals. John Wiley & Sons Inc. New Jersey. 2004. 412 p.

2. A.A. Trukhachev. Radiolokatsionnye signaly i ih primenenie (Radar signals and their applications). М. Voenizdat. 2005. 320 p.

3. M. A. Nasrabadi, M. H. Bastani. A Survey on the Design of Binary Pulse Compression Codes with Low Autocorrelation. Trends in Telecommunications Technologies. Christos J Bouras (Ed.). ISBN: 978-953-307-072-8. InTech. 2010.

4. J. Jedwab. A Survey of the Merit Factor Problem for Binary Sequences. Sequences and Their Applications. Proceedings of SETA 2004. ed. T. Helleseth et al. Lecture Notes in Computer Science. vol. 3486. pp. 30–55. Springer-Verlag. Berlin Heidelberg. 2005.

5. P. Stoica, J. Li, and M. Xue. Transmit codes and receive filters for radar. IEEE Signal Processing Magazine. vol. 25. pp. 94–109. November 2008.

6. N. Levanon. Cross-Correlation of Long Binary Signals with Longer Mismatched Filters. IEE Proceedings. Radar, Sonar, and Navigation. vol. 152. pp. 377–382. Dec. 2005.

7. R. A. Horn and C. R. Johnson. Matrix Analysis. Cambridge University Press. 1985. 652 p.

8. J. Knauer. Merit Factor Records. URL: http://www.cecm.sfu.ca/~jknauer/labs/records.html. Nov. 2004.

9. W.W. Peterson, E.J. Weldon. Error-correcting codes. MIT Press. 1972. 590 p.

10. J. Jedwab, D.J. Katz, K.U. Schmidt. Advances in the Merit Factor Problem for Binary Sequences. Journal of Combinatorial Theory. Volume 120. No 4. pp. 882-906. May 2013.

If you have any question please write: info@dspa.ru