|
“Digital
Signal Processing” No. 2-2016 |
|
Efficiency of product-codes turbo-decoding algorithms with different methods of information exchange between iterations
G.V. Zaytsev, e-mail: gennady-zaytsev@yandex.ru
A.N.Lutkov, e-mail: anlutkov@gmail.com
PSC SIC "Almaz"
Keywords: forward error correction, turbo product code,soft iterative decoding, decoding complexity.
Abstract
The article deals with Chase-Pandiah turbo decoding algorithm of product codes. To reduce computational complexity two types of algorithm modifications are suggested in the paper.
To describe standard algorithm consider product code concatenated serially from two block codes with lengths n1 and n2. Then code word of the product code may be considered as an n1 × n2 matrix, rows of which are code words of the first code and columns are code words of the second code. Turbo decoding is an iterative process consisting of carrying out a decoding of the rows followed by a decoding of the columns using soft-input soft-output (SISO) decoder of the corresponding component codes and reiterating this procedure several times. At each stage the decoder recalculates reliability estimation of each symbol, which form together n1 × n2 reliability matrix. Let Rkin and Rkout be input and output reliability matrixes at SISO stage number k. Then standard algorithm calculates the so called extrinsic information
![]()
The input for the next stage is formed by the formula
![]()
where αk+1 is a certain coefficient and initial matrix R1in = R0 is the turbo decoder input formed by soft decisions output of demodulator.
Three new modified versions of the described algorithm are suggested in the paper. In the first version formula (2) is replaced by expression:
![]() . The second variant uses the following formula instead of (1)
. The second variant uses the following formula instead of (1) ![]() . In the third version (1) is not used and the following expression is used instead of (2):
. In the third version (1) is not used and the following expression is used instead of (2):
![]() . It is shown in the paper that both bit and block error probabilities degrade insignificantly for new algorithm versions. On the other hand modified algorithms accumulate extrinsic information from all decoder stages that lead to some useful features unavailable for standard version.
. It is shown in the paper that both bit and block error probabilities degrade insignificantly for new algorithm versions. On the other hand modified algorithms accumulate extrinsic information from all decoder stages that lead to some useful features unavailable for standard version.
The second suggestion of the paper is to reduce the number of recalculated elements in SISO sub-algorithms. Error probabilities for different number of recalculated symbols are investigated in the paper for all algorithm versions. It is shown that new versions are much less sensitive to the variation of the number of recalculated symbols than standard one. For new algorithm versions this number may be reduced several fold. This fact opens the way for computational complexity reduction of the turbo decoding algorithm.
References
1. Channel coding in communication networks: from theory to turbo codes / edited by Alain Glavieux. ISTE Ltd, London, 2007.
2. G.V. Zaytsev, Poteri v otnoshenii signal/shum v sisteme svjazi ispol'zujuschei differentsial'nuju moduljatsiju i ortogonal'noe kodirovanie (Loss in Signal-to-Noise Ratio for Communication System with Binary Differential Shift Keying and Orthogonal Coding), Tsifrovaja obrabotka signalov (Digital signal processing), 2014, No. 2, pp. 15–21.
The assessment of the significance of acoustic features in the task of detecting voice activity
S.A. Kravtsov, e-mail: sk860@outlook.com
A.I. Topnikov, e-mail: topnikov@gmail.com
A.L. Priorov, e-mail: andcat@yandex.ru
The Yaroslavl State University them. P.G. Demidov (YaSU them. Demidov), Russia, Yaroslavl
Keywords: : speech signal, feature importance, voice activity detector, noise.
Abstract
The voice activity detector (VAD) is important part of any modern speech processing system. Nowadays creating robust VAD is the actual task. Was proposed the method for selection the most important acoustic features. The significance value of the spectral flatness measure (SFM), twelve mel-frequency cepstral coefficients (MFCC) and twelve gammaton-frequency cepstral coefficients (GFCC) for the voice activity detection was evaluated.
Russian-language speech database lasting 44 minutes with a sampling rate of 8000 Hz and 16 bits presentation counts was used. The total duration of the speech equal the total duration of pauses, and is 22 minutes. Before the researching, test signal was noised by additive white Gaussian noise (AWGN) with a signal / noise ratio (SNR) of -15 dB to 25 dB in steps with 5 dB.
To evaluate the significance of features we used an algorithms which based on decision trees and comparing the values of the areas under ROC-curves (AUC) for each feature. For classification were used support vector machine (SVM) with linear core, perceptron and the method of nearest neighbors. Both algorithms had the same results. As a result 7 coefficients were selected as a most importance: SFM, 1-2-5-th MFCC and 3-4-5-th GFCC. It is found that the values of features importance when the SNR of -15 dB to -5 dB differ slightly, and when the SNR of 0 dB and above the importance of these coefficients is greatly increased as compared with others. Thus, the total value of the importance of for these seven features was equal 0.55 and increased to 0.84 at 20 dB SNR. Amount importance for all attribute values at a certain SNR is equal to 1.
The second part of the work was devoted to the evaluation and comparison the classification accuracy of voice activity detectors by using extracted features and all analyzed features. In case of classification by SVM and using all coefficients the AUC was equal using selected this 7 coefficients. In case of classification by k-nearest neighbors AUC was greater when we used the most importance features.
References
1. Kravtsov S.A., Tupitsin G.S., Topnikov A.I., Sagatsiyan M.V., Priorov A.L. Issledovanie raboty detektora rechevoy aktivnosti v zadache identifikatsii diktora // Radiotekhnicheskie i telekommunikatsionnye sistemy. 2015. ¹ 4 (20). P. 61–68.
2. Kinnunen T., Rajan P. A practical, self-adaptive voice activity detector for speaker verification with noisy telephone and microphone data // ICASSP. 2013. P. 7229–7233.
3. Tazi E.B., Benabbou A., Harti M. Voice activity detection for robust speaker identification system // Spec. Issue Int. J. Comput. Appl. Softw. Eng. Databases Expert Syst. – SEDEXS. 2012. ¹ 9. P. 35–39.
4. Matveev Y.U. Tekhnologii biometricheskoj identifikatsii lichnosti po golosu i drugim modal'nostyam // Vestnik MGTU im. N.E. Baumana. Ser. «Priborostroenie». 2012. ¹ 3. P. 46–61.
5. Pasanen A. Voice activity detection in noise robust speech recognition // Theses, Tampere Univ. Technol. 2002.
6. Johnston J. Transform coding of audio signals using perceptual noise criteria // Sel. Areas Commun. IEEE. 1988. Vol. 6, ¹ 2. P. 314–323.
7. Kinnunen T., Chernenko E. Voice activity detection using MFCC features and support vector machine // Int. Conf. Speech. 2007. Vol. 2. P. 555–561.
8. Kravtsov S.A., Topnikov A.I., Priorov A.L. Detektor rechevoy aktivnosti na osnove golosuyushchih modeley gaussovskih smesey // Elektromagnitnye volny i elektronnye sistemy. 2015. Vol. 20, ¹ 8. P. 29–34.
9. Kravtsov S.A., Topnikov A.I. Analiz raboty lineynyh klassifikatorov v zadache detektirovaniya rechevoy aktivnosti // Tsifrovaya obrabotka signalov i ee primenenie. Dokl. 18-y mezhdunar. konf. 2016. T. 1. P. 403–409.
10. Cooper D. Speech detection using gammatone features and one-class support vector machine // Dis. University of Central Florida Orlando. 2013.
11. Gudnason J., Brookes M. Voice source cepstrum coefficients for speaker identification // Acoust. Speech Signal Process. 2008. ICASSP 2008. IEEE. 2008. P. 4821–4824.
12. Tazi E., Benabbou A., Harti M. Efficient text independent speaker identification based on GFCC and CMN methods // Multimed. Comput. Syst. (ICMCS). 2012 Int. Conf. on. IEEE. 2012. P. 90–95.
13. Wong E., Sridharan S. Comparison of linear prediction cepstrum coefficients and mel-frequency cepstrum coefficients for language identification // Intell. Multimedia, Video Speech Process. 2001. P. 95–98.
14. Moattar M., Homayounpour M. A simple but efficient real-time voice activity detection algorithm // Signal Process. Conf. Eur. IEEE. 2009. P. 2549–2553.
15. Sokolov E. Seminary po reshayushchim derev'yam // machinelearning.ru.
Principles of construction and effectiveness analysis of operation of wireless sensor networks based on compressive sensing theory
Parfenov V.I., e-mail: vip@phys.vsu.ru
Golovanov D.Y., e-mail: golovanov@amm.vsu.ru
Keywords: wireless sensor network, Compressive Sensing, sparse signal, bayesian algorithm, Compressive Sampling Matching Pursuit (CoSaMP), dispersion of estimation, probability of miss, probability of false alarm.
Abstract
It is shown, that principles of construction and operation of wireless sensor networks can be based on decision of estimation task of locations and number of nonzero components of some sparse vector. Some estimation algorithms based on information collected in central node of network are considered: algorithm, based on classical bayesian approach and some «greedy» algorithms, developed in Compressive Sensing theory. Behavior of different estimation characteristics in dependence of signal to noise ratio, compression ratio and sparsity of signal is investigated.
References
1. Hu F., Cao X. Wireless sensor networks: principles and practice. CRC Press, 2012. – 503 p.
2. Faludi R. Building wireless sensor networks. O’Really Media, USA, 2011. – 301 p.
3. Dargie W., Poellabauer C. Fundamentals of wireless sensor network: theory and practice. John Wiley And Sons Ltd., United Kingdom, 2010. – 311 p.
4. Eldar C., Kutyniok G. Compressed sensing: theory and applications. Cambridge University Press, 2012. – 555 p.
5. Foucart S., Rauhut H. A mathematical introduction to compressive sensing. Berlin: Springer, 2013. – 625 p.
6. Candes E., Wakin M. An introduction to compressive sampling // IEEE Signal Processing Magazine. Vol. 25, ¹2, 2008. – P. 21 – 30.
7. Baraniuk R. Compressive sensing // IEEE Signal Processing Magazine. Vol. 24, ¹4, 2007. – P. 118 – 121.
8. Donoho D. Compressed sensing // IEEE Transaction on Information Theory. Vol. 52, ¹4, 2006. – P. 1289 – 1306.
9. Tropp J., Gilbert A. Signal recovery from random measurements via orthogonal matching pursuit // IEEE Transaction on Information Theory. Vol. 53, ¹12, 2007. – P. 4655 – 4666.
10. Cai T., Wang L. Orthogonal matching pursuit for sparse signal recovery with noise // IEEE Transaction on Information Theory. Vol. 57, ¹7, 2011. – P. 4680 – 4688.
11. Needell D., Vershynin R. Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit // IEEE Journal of Selected Topics in Signal Processing. Vol. 4, ¹2, 2010. – P. 310 – 316.
12. Needell D., Tropp J. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples // Applied and Computational Harmonic Analysis. Vol. 26, ¹3, 2009. – P. 301 – 321.
13. Parfenov V.I., Golovanov D.Y. Opredelenie nezanyatih chastotnih polliapazonov po sjatim izmereniyam // Infokommunikachionnie tehnologii. V.13, ¹3, 2015. – P. 305 – 312.
14. Parfenov V.I., Golovanov D.Y. Effectivnoste ochenki vremennogo polojeniya sverhcorotkogo signala s ispolzovaniem algoritma, osnovannogo na teorie Compressive Sensing // Vestnic Voroneg. Gos. Universitita.Ser.: Fizika, matematika, ¹1, 2015. – P. 27 – 36.
15. Xiong W., Cao J., Li S. Sparse signal recovery with unknown signal sparsity // EURASIP Journal on Advances in Signal Processing. Vol. 2014, ¹1, 2014.
The methods of linear frequency and nonlinear frequency modulation signals detection with stabilization of false detection probability
K.A. Elagina, e-mail: ksenia_elagina@mail.ru
Scientific and Research Institute of Measurement Instrumentation – Novosibirsk Plant named after Komintern
Keywords: weighting, linear frequency modulation signal, nonlinear frequency modulation signal, losses of the detection, false detection probability, side lobes, normalization, double-channel processing, running by length window, censoration.
Abstract
To solve the problem of losses decrease which are induced of a weighting with simultaneously decrease of level of side lobes power signals influence on detection of signals from low-sized objects, the detector of linear frequency modulation signal and with stabilization offalse detection probability is offered.
As a nonlinear frequency modulation signal, signal with relatively low level of side lobes synthesized by author is used. Losses on weighting intime domain are absent for such signal.
In the offered detectors to stabilize of false detection probability, normalization of signal power to estimation mean signal power in running by length window, is used.
Due to great dependence of compressed nonlinear frequency modulation signal form on Doppler translation, it is offered to use a channel bank matched filter. Comparison of detectors efficiency is provided in wide range of Doppler frequencies.
It is obtained that using of detector of nonlinear frequency modulation signal and with a channel bank matched filter in all range of Doppler frequencies, is not efficient due to value of additional loss by detection of low-speed objects and also instrument cost, low efficiency when signals with different Doppler frequency collide.
It is offered to divide concerned Doppler frequency band (-140…140 KHz) on sub-bands and use different signal types and corresponding detectors in each sub-band.
To detect aerodynamic objects for Doppler frequencies -12,5…12,5 KHz in the absence powerful signals from local objects it is proposed to use the detector with nonlinear frequency modulation signal and single-channel matched filter. It is possible to obtain the gain of threshold signal value of 1,5…3,5 dB with respect to a non- weighted linear frequency modulation signal detector (with respect to a linear frequency modulation signal detector and weighting by Hamming – to 2 dB). A dual-channel linear frequency modulation signal detector is recommended in case of powerful signals from local objects.
In the case if Doppler frequencies of detected and/or overlapping in time band signals from objects lying in bands -140…12,5 KHz and 12,5…140 KHz, dual-channel linear frequency modulation signal detector is recommended. It is obtained that gain of nonlinear frequency modulation signal detector and with a single-channel matched filter might be 2…10 dB (power of filter input noise signal is 20 dB), and gain of nonlinear frequency modulation signal detector and with a multi-channel matched filter is 1…2 dB and more.
References
1. Kuk CH., Bernfel'd M. Radar signals. - M.: Sovetskoe radio, 1971. – p. 205.
2. Kobzarev YU.B. The modern radiolocation. - M.: Sovetskoe radio, 1969. – p.235.
3. Handbook. Radio electronics systems: foundation of construction and theory./ Pod red. YA.D.SHirmana. - M.: Radiotekhnika, 2007. – p.306.
4. Tel'minov O.A. The long-term methods of probing signal frequency modulation for problem of radarimages synthesis // Materialy 5-j Mezhdunarodnoj konferencii «Cifrovaya obrabotka signalov i eyo primenenie» DSPA-2003. – C.1-4.
5. Bessonova E.V., Irhin V.I. Decrease of side lobe level of anautocorrelation function of compound signals // Trudy XV nauchnoj konferencii po radiofizike. – NNGU, 2011. – pp.131–133.
6. Anan'ev A.V., Bezuglov D.A., YUhnov V.I. Increasing of noise immunity of narrow-band channels in terms of using signals with chirp modulation // Sovremennye problemy nauki i obrazovaniya. – 2013. – no.1. – pp. 1–9.
7. Eyung W.Kang Radar system, analysis, design, and simulation. - 2008. – pp.281–289. ISBN-13: 978-1-59693-347-7.
8. Patent 2518052 Russia, MPK G01S 13/00. METHOD OF STABILISING FALSE ALARM PROBABILITY (VERSIONS) AND DEVICE FOR REALISING SAID METHOD/ Belyaev B.G., ZHibinov V.A., Prudnikov S.A. (Russia) - ¹ 2012139914/07; zayavl.18.09.12; opubl.10.06.2014.
9. Patent 2585257 Russia, MPK G01S 7/36. // METHOD FOR DOUBLE-CHANNEL DETECTION OF RADAR SIGNALS WITH FALSE ALARM PROBABILITY STABILISATION/ Elagina K.A., Aksel'rod G.Z. (Russia) - ¹ 2015117986/07; zayavl.13.05.15; opubl. 27.05.2016.
10. Foundation of construction of radio engineering troops radar / Pod red. V.N.Tyapkina. - Krasnoyarsk,Sib.feder un-t, 2011. – pp.466, 471-473.
11. Lozovskij I.F. Algorithm of signals censoration in case of power heterogeneous noise. - Voprosy radioehlektroniki, no.3, 2002. – pp.97-106.
12. Aksel'rod G.Z., Elagina K.A. Use of nonlinear frequency signal for losses of the detection increase. - Izvestiya vysshih uchebnyh zavedenij Rossii. Radioehlektronika, no.2, 2015. – pp.40-43.
13. Nitzberg R. Analysis of the arithmetic mean CFAR normaliser for fluctuating targets / Nitzberg R. // IEEE Trans. vol.AES-14. –1978, Jan.
Direct digital frequency synthesizer based on inverse discrete Walsh transform
A.I. Smekalov., e-mail:
aismekalov@narod.ru
V.I. Djigan., e-mail: djigan@yandex.ru
National Research University of Electronic Technology (MIET), Russia, Moscow
Keywords: direct digital frequency synthesis, harmonic signal, cosine, sine, orthonormal basis of Walsh functions, direct and inverse discrete Walsh transform, spectral spurious components, normalized mean-square error.
Abstract
The paper considers a direct digital frequency synthesizer with a phase-cosine converter based on inverse discrete Walsh transform. Such converter allows to exclude large memory blocks and/or multipliers by replacing them with logic elements and adders and get the specified quality of the generated harmonic signal.
The output discrete harmonic signal is calculated as the sum of the expansion coefficients of the harmonic function over the Walsh basis weighted by the values of the orthonormal basis of the discrete Walsh functions. The Walsh basis is easily generated from the current phase value produced by phase accumulator, with minor hardware cost by binary logical exclusive OR (XOR operation). Algorithm based on Gray code can be used to define the relationship between phase and any Walsh function. Formed Walsh functions are used as control signals for the signed inverters. The set of signed expansion coefficients is pre-calculated according to the direct discrete Walsh transform. The outputs of inverters are summed, forming the recovered cosine.
An example of cosine decomposition over Walsh basis, calculation and analysis of Walsh expansion coefficients are also given. Only a small part of the coefficients has considerable weight in the basis. The best criterion for selection of coefficients is the choice of the first N maximum coefficients by magnitude. The coefficient distribution by bit width demonstrates a way of the following simplification of phase-cosine converter.
The proposed Walsh and classical memory synthesizers were described by Verilog language and compiled for the FPGA xc7vx690tffg1761-2 of Virtex-7 family. The proposed Walsh phase-cosine converter requires about five times less resources compared to the classic memory phase-cosine converter at the same level of spurious free dynamic range more than 100 dB. The proposed Walsh direct digital synthesizer is recommended for implementation on programmable logic or application specific integrated circuits.
References
1. Frequency synthesizers: Texbook. Shakhtarin B.I., Prokhladin G.N., Ivanov A.A., Bykov A.A., Chechulina A.A., Grechishchev D.U. Ìoscow: Goryachaya Linia Telecom, 2007. 128 p.
2. Tierney J., Rader C.M., Gold B. A digital frequency synthesizer // IEEE Transactions on Audio and Electroacoustics. 1971. Vol. 19. No. 3. P. 48–57.
3. Smekalov A.I. Metod pryamogo fazovogo sinteza siganala. Analiz i matematicheskoe modelirovanie // Radiotekhnika. 2011. No. 1. P. 16-29.
4. Smekalov A.I., Djigan V.I. Primenenie lineynoy interpolyatsii signaka v pryamom tsifrovom sinteze chastot // Telekommunikatsii. 2015. No.9. P. 2-7.
5. Djigan V.I., Smekalov A.I. Tsifrovoy sintezator s pryamim vichisleniem garmonicheskogo signala // Izvestia visshih uxhebnih zavedeniy. Elektronica. 2015. Vol. 20. No. 6. P. 625-633.
6. Kampik M., Popek G. Low-spur numerically controlled oscillator using Taylor series approximation // XI International PhD Workshop OWD 2009.
7. Wheatley C.E., Phillips D.E. Spurious suppression in direct digital synthesizers // Proceedings of the 35th Annual Frequency Control Symposium. 1981. P. 428.
8. Sunderland D.A. CMOS/SOS frequency synthesizer LSI circuit for spread spectrum communications // IEEE Journal of Solid-State Circuits. 1984. Vol. SC-19. No. 4. P. 497-506.
9. Golubov B.I., Efimov A.V., Skvortsov V.A. Walsh series and transformations: theory and applications. Moscow: Nauka, 1987. 352 p.
10. Smekalov A.I. Primenenie bazisa funktsiy Uolsha v tsifrovom sinteze chastot // 18-ya Mezhdunarodnaya konferentsia “Tsifrovaya obrabotka siganlov i ee primenenia - DSPA-2016”. Moscow, 2016. Vol. 2. P. 793-798.
11. Smekalov A.I. Realizatsia tsifrovogo sintezatora chastor na osnove bazisa funktsiy Uolsha // Mezdunarodnaya konferentsia “Radioelektronnie ustroystva I sistemi dlya infokommunikatsionnih tehnologiy - REDS-2016”. Moscow, 2016. Vol. 1. P. 127-132.
12. Ugryumov E.P. Digital circuit design: Texbook. 2nd ed. St. Petersburg: BHV-St Petersburg, 2007. 800 p.
13. URL: http://www.xilinx.com (access date: 29.05.2016).
Integer design of IIR Filters with difficult selective requirements
V.N. Bugrov, e-mail: bug@rf.unn.ru
N.I. Lobachevsky state university of Nizhni Novgorod (NNSU) , Russia, N.Novgorod
Keywords: the integer IIR-filter, integer nonlinear programming, multifunctional synthesis, criterion function.
Abstract
Currently, there are many applied problems of digital filtration with the highly complex requirements of frequency selection. The highest possible satisfaction of such complex selective requirements are known, IIR filters. However, the classical methods of designing recursive digital filters via analog prototype using the method of bilinear transformation does not allow to synthesize IIR filters with complex, arbitrary shape frequency response, make it impossible to meet the ever-increasing selective demand. Material reporting format under bilinear transformation forced to quantize their values, which leads to the well-known undesirable for the operation of this IIR filter effects.
The possibility of direct synthesis of digital IIR filters with complex selective requirements directly in an integer state space can be provided by the methodology integer nonlinear programming. This ideology allows for the efficient design of the integer recursive filters with a given number of bits represent data at the highest performance requirements of aggregate frequency characteristics of the filter at any form of their assignment.
This article discusses issues integral simulation and synthesis of recursive (IIR) digital filters taking into account the capacity to implement them on digital platforms with integer arithmetic calculations. The problem statement and solution of multifunctional synthesis of digital filters such a problem on the basis of the numerical methods of integer nonlinear mathematical programming are given. As an several typical examples, the problem solution of synthesis of IIR-filters with difficult selective requirements has been given. The analysis of their characteristics is resulted.
References
1. Bugrov V.N. Development of digital filters by methods of integer nonlinear programming. // Vestnik Newsletter NNSU, 2009, ¹ 6. p. 61 – 70.
2. Shkelev E.I., Bugrov V.N., Proidakov V.I., Artemev V.V. Integer digital filters - effective solution for 8-bits digital platforms. Moscow, Components and technologies, ¹ 10, 2013, p. 104 – 110.
3. Bugrov V.N., Proidakov V.I., Artemev V.V. Search design technology integer digital filters. Part 1, Moscow, Components and technologies, ¹ 10, 2013, p. 104 – 110.
4. Bugrov V.N., Proidakov V.I., Artemev V.V. Search design technology integer digital filters. Part 2, Moscow, Components and technologies, ¹ 8, 2014, p. 43 – 49.
5. Bugrov V.N., Proidakov V.I., Artemev V.V. Search design technology integer digital filters. Part 3, Moscow, Components and technologies, ¹ 1, 2015, p. 154 – 159.
6. Bugrov V.N., Proidakov V.I., Artemev V.V. Synthesis of digital filters by methods of integer nonlinear programming. 17-th international conference "Digital signal processing and its applications – DSPA-2915", Abstracts. M: NTO RES them. A. S. Popov, 2015, p. 200 – 204.
7. Demðster A.G., Macleod M.D. IIR digital filter design using minimum adder multiplier blocks.//IEEE Trans.on Circuits and Systems-II, 1998, v. 45, N 6.
8. Voinov B.S., Bugrov V.N., Voinov B.B. Informacionnie tekhnologii i sistemi: poisk optimalnih, originalnih i racionalnih resheniy. Moscow.: Science, 2007, 730 p.
9. Artemev V.V., Bugrov V.N. IIR filter design with phase linearity. Moscow, Components and technologies, ¹ 7, 2013, p. 132-134.
10. Bugrov V.N. Integer design of the Gaussian digital filters. // Vestnik Newsletter NNSU, 2012, ¹ 3. p. 49 – 54/
11. Mingazin A.T. Synthesis of IIR-filters of low complexity with characteristics similar to those of the Gaussian curve. Moscow, Components and technologies, ¹ 11, 2013, p. 144 – 148.
12. Jaconia B.E. TV. Moscow, Hot line – Telecom, 2007,618 p.
13. Briliantov D.P., Kulikov B.N., Roxman M.A. Portable color TVs. Moscow, Radio and communication, 1989, 306 p.
14. Rabiner R, Gold B. Theory and application of digital signal processing. Moscow, Mir, 1978, 848 p
15. Ifeachor E., Jervis B. Digital signal processing. A practical approach. Moscow.: "Wiliame", 2004, 992 p.
16. Mingazin A.T. Synthesis of IIR-filters of low complexity with characteristics similar to those of the Gaussian curve. Moscow, DSPA, 2002. Vol.1. p. 90-93.
Filter banks for broadband data tranmission systems
Vityazev V.V., e-mail: vityazev.v.v@rsreu.ru
Keywords: broadband data transmission, filter banks, frequency selection, subband processing, comb filtering, multistage structure.
Abstract
Problem of constructing filter banks for high speed broadband data transmission systems is considered. The problem is mentioned to be very actual. Comparative analysis of filter banks efficiecy is conducted depending on the required computational costs, data memory size and insertion delay. The best result is achieved when the multistage pyramidal form of filter banks construction is used. Multistage pyramidal form allows to reduce computational costs in three times compared to forward form and time compared to fast convolution.
In this paper a particular example is considered to illustrate the efficiency of various methods of digital bandpass filter (DBF) bank design. 64-channel filter system is designed with squareness ratio of filter amplitude-frequency characteristic α = 10 and the permissible deviations from the desired frequency response ε1perm=10-2 and ε2perm=10-3. The sampling frequency of the input complex signal ƒS = 10 kHz.
The results of the calculations are presented in Table 1.
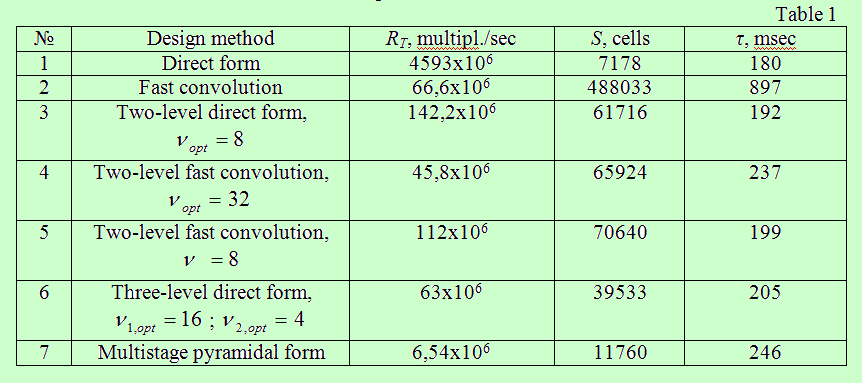
RT – the number of multiplication operations per time unit, S – the number of the data memory cells, τ – the delay time.
The analysis of the presented results of the costs calculation for the implementation of the DBF set with the frequency selection desired properties allows to draw the following conclusions.
1. The direct form of implementation without preliminary transformations is characterized by the minimum capacity of the data memory and the minimum delay. This is the simplest form of implementation in terms of the input data processing algorithm and structure chart! But this is the most unprofitable form from the position of computational costs (two or three orders in relation to the optimal solution). The above computational costs increase proportional to the square of the M-number of frequency channels.
2. Fast convolution assumes that each DBF is constructed using a double fast Fourier transform (the inverse transform is performed separately for each frequency channel), that allows to reduce the computational costs by almost two orders. But the transition to block data processing and the forced use of the buffering mechanism lead to multiple increase the capacity of the data memory (by two orders) and delay (five times).
3. The transition to the two- and three-level implementation of the DBF set with preliminary processing using digital comb filters gives the ability to reduce the computational costs by two orders to the direct form of realization (with the optimal values of the decimation coefficients of their impulse response) and reduce by an order the capacity of data memory and by 3-5 times delay in relation to fast convolution (without conceding in processing rate).
4. By a set of criteria (and the first of all by the required computational costs) the best solution of the objective provides a multistage pyramidal form of implementation, first published in [7]. In case of commensurable costs on data memory and delay in relation to direct form, the multistage pyramidal implementation allowed to reduce the given computational costs by almost three orders and by an the order in relation to fast convolution.
References
1. Behrouz Farhang-Boroujeny. OFDM Versus Filter Bank Multicarrier // IEEE Signal Processing Magazine, -2011, -Vol. 28, ¹ 3, -P. 92-112.
2. Lin L. and Farhang-Boroujeny B. Cosine modulated multitone modulation for very high speed digital subscriber lines // EURASIP J. Appl. Signal Processing, -2006, Aprticle ID 19329.
3. Vityazev V.V., Ovinnikov A.A. Metody analiza/sinteza v sistemah besprovodnoi svyazi so mnogimi nesushimi // Jelekrosvjaz. 2013. ¹ 9 . – S. 28-32.
4. Vityazev V.V. Digital frequency selection of signals. Ì.: Radio and telecommunication, 1993. 240 p.
5. Vityazev V.V., Muraviev S.I., Stepashkin A.I. Metod sinteza cifrovyh uzkopolosnyh KIH-filetrov // Izvestya vuzov. Radioelektronika. – 1981. – Ò. 24, ¹ 7. – S.. 55-59.
6. Emmanaual C. Ifeachor, Barrie W. Jervis. Digital Signal Processing: A Practical Approach : Prentice Hall, 2002. 992 p.
7. Vityazev V.V., Muraviev S.I . Sintez cifrovoy sistemy chastotnoy selekcii signalov na osnove polupolosneh grebenchatyh filtrov // Jelekrosvjaz. – 1988. - ¹ 3. – S.57-61.
The scaling of recursive digital filter structures using MATLAB
A.I. Solonina, e-mail: as-io@yandex.ru
Saint Petersburg State University of Telecommunications
named after prof. M. A. Bonch-Bruevich (SPbGUT),
Russia, Saint Petersburg
Keywords: structure, system function, adder, overflow, overflow mode, scaling, scaling factor, algorithm.
Abstract
Nonlinear quantization procedures in digital fixed point systems are accompanied by quantization errors. In the DSP theory each specific error is analyzed separately from any other quantization errors. Multipliers of the digital system structure provide some quantization errors known as the own noise. Paper [5] considered the own noise of recursive digital filter structures. Simple equivalent linear model and MATLAB algorithm for calculation of the own noise variance were proposed.
Adders of the digital system structure can create some quantization errors known as errors of overflow of adders. Cascade IIR filter structures with second order sections (SOS) are the most sensitive to these errors. Unlike FIR filter structures, overflow mode (Saturate or Wrap) for each sum in IIR filter structure will distort a result. The scaling allows preventing or minimizing errors of overflow.
Theoretical basis of scaling is known. However this basis does not consider many problems related to modeling the procedures by MATLAB. The report contains some additional interpretations of the existing theory allowing the user to realize the above mentioned modeling.
General principles of scaling procedures are described and main steps of scaling are substantiated. It is considered implementation of these principles for cascade structures with typical SOS: Direct-form I, Direct-form II, Direct-form I transposed, Direct-form II transposed. Each of scaling stages is illustrated by a specific SOS example with two sections. Calculation formulas for the Gains and Numerators after the scaling are derived.
The calculation of scaling factors is produced on the basis of the norm Linf for Magnitude Response. The general algorithm and his application are examined for cascade structures with typical SOS.
The paper illustrates the theoretical approach by results of IIR filter scaling using GUI FDATool.
General principles of normalizing Numerators and Gains are described and main steps of normalizing are substantiated. The paper illustrates the theoretical approach by results of IIR filter normalizing.
Simple MATLAB algorithm for calculation of the own noise variance of the cascade structure is proposed after the scaling. Calculation formulas for the own noise variance after the scaling are derived.
The cascade structure of IIR filters with known SOS structures and new Numerators is described as the dfilt object with the corresponding coefficient matrix. Coefficient matrixes of equivalent system functions are formed within the cycle by consecutive nullification of initial matrix elements. Equivalent impulse responses of cascade structure parts are calculated within the cycle with automatic limitations up to equal length. However coefficient matrices will differ before and after the scaling. As a result the own noise variance will be less after the scaling. The paper illustrates this effect for IIR filters with different SOS structures.
References
1. V Ingle, J/Proakis Digital Signal Processing Using MATLAB // Second Edition, Thomson.
2. E. Ifeachor, B. Jervis Digital Signal Processing // Moscow –: Saint Petersburg – Kiev: "Wiljams", 2004/
3. A.V. Oppenheim, R.V. Schafer Digital Signal Processing // Moscow: "Technosfera", 2006.
4. A.I. Solonina, S.M/ Arbusov Digital Signal Processing. Modeling in MATLAB // Saint Petersburg: "BHV- Petersburg", 2008.
5. A.I. Solonina Own noise estimates of recursive digital filter structures and their MATLAB calculation // Digital signal processing, 2015, ¹ 2. pp.39-46.
If you have any question please write: info@dspa.ru
